Giải bài 4.7 trang 83 SGK Toán 8 tập 1 - Kết nối tri thức
Cho tam giác ABC.
Đề bài
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh tứ giác BMNC là hình thang.
b) Tứ giác MNPB là hình gì? Tại sao?
Phương pháp giải - Xem chi tiết
a. Sử dụng tính chất đường trung bình trong tam giác ABC, sử dụng dấu hiệu nhận biết hình thang.
b. Dựa vào dấu hiệu nhận biết, xác định MNPB là hình bình hành
Lời giải chi tiết
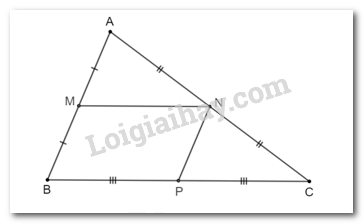
a) Vì M, N lần lượt là trung điểm của các cạnh AB, AC nên MN là đường trung bình của tam giác ABC suy ra MN // BC hay MN // BP.
Tứ giác BMNC có MN // BP nên tứ giác BMNC là hình thang (đpcm).
b) Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của tam giác ABC suy ra NP // AB hay NP // MB.
Tứ giác MNPB có MN // BP; BM // NP (chứng minh trên).
Do đó, tứ giác MNPB là hình bình hành.