Giải bài 4. 9 trang 83 SGK Toán 8 tập 1 - Kết nối tri thức — Không quảng cáo

Đề bài

Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh tứ giác AHOK là hình chữ nhật.

Lời giải chi tiết

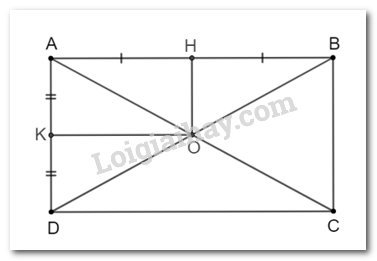
Vì ABCD là hình chữ nhật nên $\widehat {BA{\rm{D}}} = {90^o}$ và hai đường chéo AC, BD bằng nhau và cắt nhau tại trung điểm O của mỗi đường.

Suy ra AB ⊥ AD; O là trung điểm của AC và BD.

Vì O, H lần lượt là trung điểm của BD và AB nên OH là đường trung bình của tam giác ABD.

Suy ra OH // AD mà AB ⊥ AD nên OH ⊥ AB hay $\widehat {AHO} = {90^o}$

Tương tự, ta chứng minh được: OK ⊥ AD hay $\widehat {AK{\rm{O}}} = {90^o}$.

Ta có: $\widehat {BA{\rm{D}}} + \widehat {AHO} + \widehat {AK{\rm{O}}} + \widehat {HOK} = {360^o}$

90°+90°+90°+$\widehat {HOK}$=360°

270°+$\widehat {HOK}$=360°

Suy ra $\widehat {HOK}$=360°−270°=90°

Tứ giác AHOK có $\widehat {BA{\rm{D}}}$=90°;ˆAHO=90°; $\widehat {AHO}$=90°;$\widehat {AK{\rm{O}}}$=90 ^o

Do đó, tứ giác AHOK là hình chữ nhật.