Giải bài 4 trang 112 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Cho tứ diện ABCD. Trên các cạnh AB, AC, BD lần lượt lấy các điểm E, F, G sao cho \(EB > AE,AF > FC,BG > GD\). Tìm giao tuyến của các cặp mặt phẳng (EFG) và (ACD), (EFG) và (BCD), (EFG) và (ABD).
Đề bài
Cho tứ diện ABCD. Trên các cạnh AB, AC, BD lần lượt lấy các điểm E, F, G sao cho \(EB > AE,AF > FC,BG > GD\). Tìm giao tuyến của các cặp mặt phẳng (EFG) và (ACD), (EFG) và (BCD), (EFG) và (ABD).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về giao tuyến giữa hai mặt phẳng để tìm giao tuyến: Đường thẳng d chung giữa hai mặt phẳng (P) và (Q) được gọi là giao tuyến của (P) và (Q), kí hiệu \(d = \left( P \right) \cap \left( Q \right)\).
Lời giải chi tiết
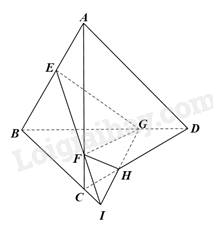
Ta có, EF là giao tuyến của hai mặt phẳng (EFG) và (ABC).
Trong mặt phẳng (ABC), gọi I là giao điểm của EF và BC.
Trong mặt phẳng (BCD), gọi H là giao điểm của IG và CD.
Vì \(\left\{ \begin{array}{l}H \in CD \subset \left( {ACD} \right),H \in IG \subset \left( {EFG} \right)\\F \in AC \subset \left( {ACD} \right),F \in FE \subset \left( {EFG} \right)\end{array} \right.\) nên giao tuyến của hai mặt phẳng (EFG) và (ACD) là FH.
Vì \(\left\{ \begin{array}{l}H \in CD \subset \left( {BCD} \right),H \in IG \subset \left( {EFG} \right)\\G \in BD \subset \left( {BCD} \right),G \in FG \subset \left( {EFG} \right)\end{array} \right.\) nên giao tuyến của hai mặt phẳng (EFG) và (BCD) là GH.
Vì \(\left\{ \begin{array}{l}E \in AB \subset \left( {ABD} \right),E \in FE \subset \left( {EFG} \right)\\G \in BD \subset \left( {ABD} \right),G \in FG \subset \left( {EFG} \right)\end{array} \right.\) nên giao tuyến của hai mặt phẳng (EFG) và (ABD) là GE.