Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Cho hai điểm B, C cố định trên đường tròn \(\left( {O;{\rm{ }}R} \right)\) và một điểm A thay đổi trên đường tròn đó
Đề bài
Cho hai điểm B, C cố định trên đường tròn \(\left( {O;{\rm{ }}R} \right)\) và một điểm A thay đổi trên đường tròn đó. Chứng minh trực tâm H của tam giác ABC luôn nằm trên một đường tròn cố định.
Phương pháp giải - Xem chi tiết
Ta đi chứng minh trực tâm H của tam giác ABC luôn nằm trên ảnh của đường tròn \(\left( {O;{\rm{ }}R} \right)\) qua phép tịnh tiến theo \(\overrightarrow {B'C} \)
Lời giải chi tiết
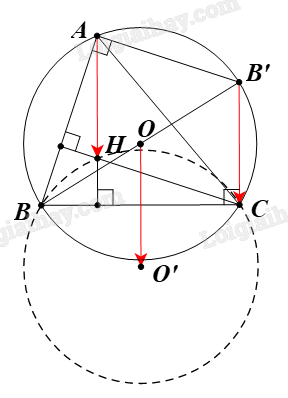
Kẻ đường kính BB’.
Do B, C cố định trên (O) nên B’, C cũng cố định trên (O).
Suy ra \(\overrightarrow {B'C} \) là vectơ không đổi.
Ta có \(\widehat {BCB'} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn (O)).
Suy ra \(BC \bot B'C.\)
Mà \(AH \bot BC\) (do H là trực tâm của ∆ABC).
Do đó \(AH//B'C\,\,\left( 1 \right)\)
Chứng minh tương tự, ta được \(AB'//CH{\rm{ }}\left( 2 \right)\)
Từ (1), (2), suy ra tứ giác AHCB’ là hình bình hành.
Suy ra \(AH{\rm{ }} = {\rm{ }}B'C.\)
Mà \(AH{\rm{ }}//{\rm{ }}B'C\) (chứng minh trên).
Vì vậy \(\overrightarrow {AH} = \overrightarrow {B'C} \)
Do đó \(H = {T_{\overrightarrow {B'C} }}\left( A \right)\).
Vậy khi A thay đổi trên đường tròn (O) thì trực tâm H của tam giác ABC luôn nằm trên ảnh của đường tròn (O) là đường tròn (O’) qua \({{\rm{T}}_{\overrightarrow {B'C} }}\).