Giải bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
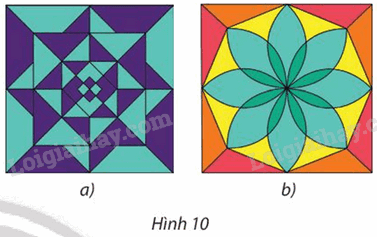
Chỉ ra phép quay có thể biến mỗi hình trong Hình 10 thành chính nó.
Đề bài
Chỉ ra phép quay có thể biến mỗi hình trong Hình 10 thành chính nó.
Phương pháp giải - Xem chi tiết
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết
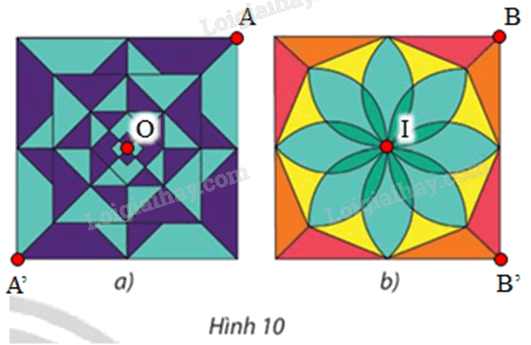
⦁ Hình 10a:
Hình vẽ có dạng hình vuông, gọi O là tâm hình vuông đó và A là 1 đỉnh của hình vuông.
Phép quay tâm O, góc quay 180° biến điểm A thành điểm A’.
Tương tự, ta chọn các điểm khác bất kì trên Hình 10a.
Khi đó qua phép quay tâm O, góc quay 180° ta cũng xác định được ảnh của các điểm đó trên Hình 10a ban đầu.
Vậy phép quay biến Hình 10a thành chính nó là phép quay tâm O, góc quay 180°.
Ngoài ra, phép quay tâm O, góc quay –180° cũng biến Hình 10a thành chính nó.
⦁ Hình 10b:
Hình vẽ có dạng hình vuông, gọi I là tâm hình vuông đó và B là 1 đỉnh của hình vuông.
Phép quay tâm I, góc quay 90° biến điểm B thành điểm B’.
Tương tự, ta chọn các điểm khác bất kì trên hình 10b.
Khi đó qua phép quay tâm I, góc quay 90° ta cũng xác định được ảnh của các điểm đó trên Hình 10b ban đầu.
Vậy phép quay biến Hình 10b thành chính nó là phép quay tâm I, góc quay 90°.
Chú ý: Có nhiều phép quay biến Hình 10a thành chính nó, chẳng hạn ngoài phép quay ở trên, ta có thể kể đến phép quay tâm I, góc quay 180° hoặc phép quay tâm I, góc quay –90°, …