Giải Bài 4 trang 49 sách bài tập toán 7 - Chân trời sáng tạo — Không quảng cáo

Đề bài

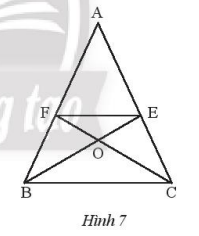
Cho hình 7, biết AB = AC và BE là tia phân giác của $\widehat {ABC}$, CF là tia phân giác của góc $\widehat {ACB}$. Chứng minh rằng:

a) $\Delta ABE = \Delta ACF$

b) Tam giác OEF cân

Lời giải chi tiết

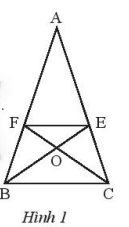
a) ta có AB = AC nên tam giác ABC cân tại A suy ra $\widehat B = \widehat C$

Mặt khác: $\widehat {FCA} = \frac{{\widehat C}}{2}$ (vì  CF là tia phân giác của góc $\widehat {ACB}$)

$\widehat {EBA} = \frac{{\widehat B}}{2}$ (vì BE là tia phân giác của $\widehat {ABC}$)

Vậy $\widehat {FCA} = \widehat {EBA}$

Xét tam giác ACF và tam giác ABE có:

$\widehat {{A^{}}}$chung

AC = AB

$\widehat {FCA} = \widehat {EBA}$

Suy ta: $\Delta ACF = \Delta ABE(g - c - g)$

b) Ta có: $\Delta ACF = \Delta ABE(g - c - g)$suy ra: BE = CF (1)

Ta lại có tam giác OBC cân tại O suy ra OB = OC (2)

Từ (1) và (2) suy ra BE – OB = CF – OC nên OE = OF

Vậy tam giác OEF cân tại O.