Giải Bài 4 trang 60 sách bài tập toán 7 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho tam giác ABC có ba trung tuyến AM, BN, CP đồng quy tại G. Chứng minh: $GA + GB + GC = \frac{2}{3}\left( {AM + BN + CP} \right)$

Lời giải chi tiết

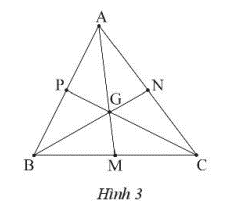
Ta có G là trọng tâm tam giác ANC, do đó ta có:

$GA = \frac{2}{3}AM;GB = \frac{2}{3}BN;GC = \frac{2}{3}CP$

Suy ra: $GA + GB + GC = \frac{2}{3}\left( {AM + BN + CP} \right)$