Giải Bài 4 trang 63 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác ABC có \(\widehat {{A^{}}} = {65^o},\widehat B = {54^o}\). Vẽ trực tâm H của tam giác ABC, Tính góc AHB.
Đề bài
Cho tam giác ABC có \(\widehat {{A^{}}} = {65^o},\widehat B = {54^o}\). Vẽ trực tâm H của tam giác ABC, Tính góc AHB.
Phương pháp giải - Xem chi tiết
Phương pháp
- Sử dụng: tính chất ba đường cao trong tam giác.
- Áp dụng: tổng ba góc trong một tam giác bằng \({180^o}\)
Lời giải chi tiết
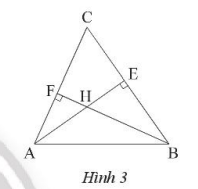
Ta có H là giao điểm của hai đường cao AE và BF.
Trong tam giác vuông ABE ta có:
\(\widehat {E{\rm{A}}B} = {90^o} - \widehat B = {90^o} - {54^o} = {36^o}\)
Trong tam giác vuông BAF ta có:
\(\widehat {FBA} = {90^o} - \widehat {{A^{}}} = {90^o} - {65^o} = {25^o}\)
Trong tam giác AHB ta có:
\(\widehat {AHB} = {90^o} - {36^o} - {25^o} = {119^o}\)
Cùng chủ đề:
Giải Bài 4 trang 63 sách bài tập toán 7 - Chân trời sáng tạo