Giải bài 4 trang 72 sách bài tập toán 8 - Chân trời sáng tạo
Cho tam giác ABC cân tại A \(\left( {\widehat A < {{90}^0}} \right)\), các đường cao BD và CE cắt nhau tại H.
Đề bài
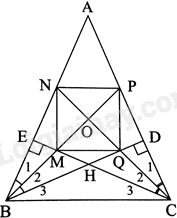
Cho tam giác ABC cân tại A \(\left( {\widehat A < {{90}^0}} \right)\), các đường cao BD và CE cắt nhau tại H. Tia phân giác của góc ABD cắt EC và AC lần lượt tại M và P. Tia phân giác của góc ACE cắt BD và AB lần lượt tại Q và N. Chứng minh rằng:
a) \(\widehat {ABD} = \widehat {ACE}\);
b) \(BH = CH;\)
c) Tam giác BOC vuông cân;
d) MNPQ là hình vuông.
Phương pháp giải - Xem chi tiết
a) Sử dụng tính chất của hai góc phụ nhau để chứng minh.
b) Sử dụng kiến thức về tính chất tam giác cân để chứng minh: Tam giác cân có hai cạnh bên bằng nhau.
d) Sử dụng kiến thức về dấu hiệu nhận biết hình vuông để chứng minh: Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
Lời giải chi tiết
a) Tam giác ABD vuông tại D nên \(\widehat {ABD} + \widehat A = {90^0}\)
Tam giác ACE vuông tại E nên \(\widehat {ACE} + \widehat A = {90^0}\)
Do đó, \(\widehat {ABD} = \widehat {ACE}\)
b) Tam giác ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB}\)
mà \(\widehat {ABD} = \widehat {ACE}\) nên \(\widehat {ABC} - \widehat {ABD} = \widehat {ACB} - \widehat {ACE}\)
Do đó, \(\widehat {HBC} = \widehat {HCB}\). Suy ra, tam giác HBC cân tại H. Do đó, \(BH = CH\)
c) Không có dữ kiện của điểm O trong đề bài
d) Gọi O là giao điểm của CN và BP.
Vì BO là tia phân giác của góc ABD nên \(\widehat {{B_1}} = \widehat {{B_2}} = \frac{1}{2}\widehat {ABD}\)
Vì CO là tia phân giác của góc ACE nên \(\widehat {{C_2}} = \frac{1}{2}\widehat {ACE}\)
Mà \(\widehat {ABD} = \widehat {ACE}\) (cmt) nên \(\widehat {{B_2}} = \widehat {{C_2}}\).
Do đó, \(\widehat {{B_2}} + \widehat {{B_3}} = \widehat {{C_2}} + \widehat {{C_3}}\) hay \(\widehat {OBC} = \widehat {OCB}\). Suy ra, tam giác BOC cân tại O. Do đó, \(OB = OC\)
Ta có: \(\widehat {{B_1}} = \widehat {{C_2}}\left( { = \widehat {{B_2}}} \right)\) nên ta có:
\(\widehat {{B_3}} + \widehat {{B_2}} + \widehat {{C_2}} + \widehat {{C_3}} = \widehat {{B_3}} + \widehat {{B_2}} + \widehat {{B_1}} + \widehat {{C_3}} = {180^0} - \widehat {BEC} = {90^0}\)
Do đó, \(\widehat {BOC} = {90^0}\) nên \(BO \bot NQ\)
Tam giác BMH và tam giác CQH có:
\(\widehat {{B_2}} = \widehat {{C_2}}\) (cmt), \(BH = CH\) (cmt), \(\widehat {BHM} = \widehat {CHQ}\) (hai góc đối đỉnh). Do đó, \(\Delta BMH = \Delta CQH\left( {g - c - g} \right)\). Suy ra: \(BM = CQ\)
Do đó, \(OB - BM = OC - QC\) nên \(OM = OQ\) (1)
Tam giác BNQ có BO là đường cao đồng thời phân giác đồng thời là đường cao nên tam giác BNQ cân tại B.
Suy ra, BO là đường trung tuyến nên \(ON = OQ\) (2)
Chứng minh tương tự ta có: \(OM = OP\) (3)
Từ (1), (2) và (3) ta có: \(OM = OQ = OP = ON\)
Do đó, \(ON + OQ = OM + OP\) hay \(NQ = MP\)
Tứ giác MNPQ có: \(OM = OP;OQ = ON\) nên MNPQ là hình bình hành, mà \(NQ = MP\) nên MNPQ là hình chữ nhật. Lại có: \(MP \bot NQ\) nên MNPQ là hình vuông.