Giải bài 4 trang 78 SGK Toán 7 tập 2 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho tam giác nhọn ABC có ba đường cao AD, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.

Lời giải chi tiết

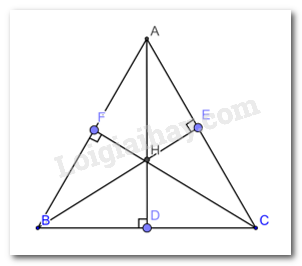
Xét tam giác BFC và tam giác CEB có:

BC chung

FC = BE

$\widehat {BFC} = \widehat {BEC} = {90^o}$

$\Delta BFC = \Delta CEB$ ( cạnh huyền – cạnh góc vuông)

$\Rightarrow \widehat C = \widehat B$ (2 góc tương ứng) (1)

Xét tam giác CFA và tam giác ADC ta có:

CF = AD

AC chung

$\widehat {ADC} = \widehat {AFC} = {90^o}$

$\Delta CFA = \Delta ADC$ (cạnh huyền – cạnh góc vuông)

$\Rightarrow \widehat C = \widehat A$ (2 góc tương ứng) (2)

Từ (1) và (2) $\Rightarrow \widehat C = \widehat A = \widehat B$ $\Rightarrow$ Tam giác ABC là tam giác đều do có 3 góc bằng nhau