Giải bài 4 trang 82 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho nửa đường tròn (O; R) có BC là đường kính. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF, Bx của nửa đường tròn (O) (F là tiếp điểm), tia AF cắt tia Bx tại D. Chứng minh OBDF là tứ giác nội tiếp.
Đề bài
Cho nửa đường tròn (O; R) có BC là đường kính. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF, Bx của nửa đường tròn (O) (F là tiếp điểm), tia AF cắt tia Bx tại D. Chứng minh OBDF là tứ giác nội tiếp.
Phương pháp giải - Xem chi tiết
Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn.
Lời giải chi tiết
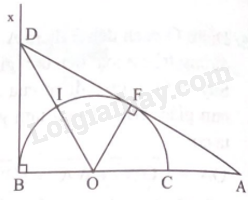
Ta có \(\widehat {DBO} = {90^o}\) và \(\widehat {DFO} = {90^o}\)(tính chất của tiếp tuyến).
Gọi I trung điểm của DO.
Tam giác DBO vuông tại O nên nội tiếp đường tròn tâm I, bán kính bằng \(\frac{1}{2}DO\).
Tương tự, tam giác DFO vuông tại F nên nội tiếp đường tròn tâm I, bán kính bằng \(\frac{1}{2}DO\).
Do đó, tứ giác OBDF nội tiếp đường tròn tâm I, bán kính bằng \(\frac{1}{2}DO\).