Giải bài 4 trang 87 SGK Toán 7 tập 2 - Cánh diều
Cho
Đề bài
Cho \(\Delta ABC = \Delta MNP\). Gọi D, E lần lượt là trung điểm của BC và CA ; Q, R lần lượt là trung điểm của NP và PM . Chứng minh:
a) AD = MQ ;
b) DE = QR.
Phương pháp giải - Xem chi tiết
a) Chứng minh tam giác ABD bằng tam giác MNQ .
b) Chứng minh tam giác DEC bằng tam giác QRP .
Lời giải chi tiết
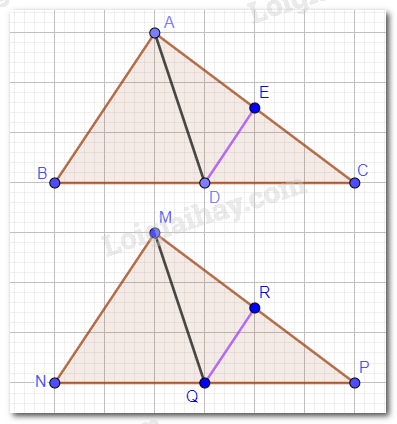
a) Xét hai tam giác ABD và tam giác MNQ :
AB = MN (do \(\Delta ABC = \Delta MNP\)).
\(\widehat {ABD} = \widehat {MNQ}\) (\(\widehat {ABD} = \widehat {MNQ}\)).
BD = NQ (\(\dfrac{1}{2}BC = \dfrac{1}{2}NP\))
BC = NP (do \(\Delta ABC = \Delta MNP\)).
Vậy \(\Delta ABD = \Delta MNQ\)(c.g.c) nên AD = MQ ( 2 cạnh tương ứng)
b) Vì \(\Delta ABC = \Delta MNP\) nên BC = NP ( 2 cạnh tương ứng) . Do đó, \(\dfrac{1}{2}BC = \dfrac{1}{2}NP\) hay DC = QP
Vì \(\Delta ABC = \Delta MNP\) nên AC = MP ( 2 cạnh tương ứng) . Do đó, \(\dfrac{1}{2}AC = \dfrac{1}{2}MP\) hay EC = RP
Xét hai tam giác DEC và tam giác QRP :
DC = QP
\(\widehat {ECD} = \widehat {RPQ}\)(\(\Delta ABC = \Delta MNP\))
EC = RP
Vậy \(\Delta DEC = \Delta QRP\)(c.g.c) nên DE = QR ( 2 cạnh tương ứng)