Giải bài 4 trang 92, 93 vở thực hành Toán 9 tập 2 — Không quảng cáo

Đề bài

Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng $\widehat {EIF} + \widehat {BAC} = {180^o}$.

Lời giải chi tiết

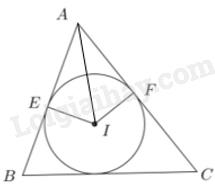
Vì các tam giác EIA và FIA lần lượt vuông tại đỉnh E và F nên $\widehat {EIA} + \widehat {IAE} = {90^o}$ và $\widehat {FAI} + \widehat {AIF} = {90^o}$.

Ta có:

$\begin{array}{l}\widehat {EIF} + \widehat {BAC} = \widehat {EIA} + \widehat {FIA} + \widehat {IAF} + \widehat {IAE}\\ = \left( {\widehat {EIA} + \widehat {IAE}} \right) + \left( {\widehat {FAI} + \widehat {AIF}} \right)\\ = {90^o} + {90^o} = {180^o}\end{array}$