Giải bài 41 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho hình lăng trụ tam giác \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh bằng \({\rm{a}}\),
Đề bài
Cho hình lăng trụ tam giác \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh bằng \({\rm{a}}\), tam giác \(AB'C'\) cân tại \(A\), mặt phẳng \(\left( {AB'C'} \right)\) vuông góc với mặt phẳng \(\left( {A'B'C'} \right)\) và \(AA' = a\sqrt 3 \).
a) Chứng minh rằng \(BCC'B'\) là hình chữ nhật.
b) Tính theo a thể tích khối lăng trụ \(ABC \cdot A'B'C'\).
c) Tính góc giữa đường thẳng \(AA'\) và mặt phẳng \(\left( {A'B'C'} \right)\).
Phương pháp giải - Xem chi tiết
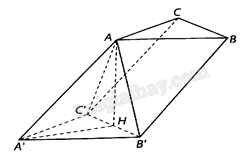
a) Kẻ \(AH\) vuông góc với \(B'C'\) tại \(H\).Chứng minh \(AH \bot \left( {A'B'C'} \right) \Rightarrow B'C' \bot AH\)
Chứng minh \(B'C' \bot \left( {AA'H} \right) \Rightarrow B'C' \bot AA'\).
Kết hợp với \(BB'//AA'\) nên \(B'C' \bot BB'\) hay \(BCC'B'\) là hình chữ nhật.
b) Tính chiều cao \(AH = \sqrt {A{A^{{\rm{'}}2}} - A'{H^2}} \).
Tính thể tích khối lăng trụ \(ABC \cdot A'B'C'\) bằng \({S_{A'B'C'}} \cdot AH\).
c) Chứng minh góc giữa \(AA'\) và mặt phẳng \(\left( {A'B'C'} \right)\) là góc giữa hai đường thẳng \(AA'\) và \(A'H\), mà \(\left( {AA',A'H} \right) = \widehat {AA'H}\).
Xét tam giác \(AA'H\) vuông tại \(H\), ta có: \({\rm{cos}}\widehat {AA'H} = \frac{{A'H}}{{AA'}} \Rightarrow \widehat {AA'H}\).
Kết luận góc giữa đường thẳng \(AA'\) và mặt phẳng \(\left( {A'B'C'} \right)\)
Lời giải chi tiết

a) Kẻ \(AH\) vuông góc với \(B'C'\) tại \(H\) thì \(AH \bot \left( {A'B'C'} \right)\) và \(H\) là trung điểm của \(B'C'\), tam giác \(A'B'C'\) đều nên \(A'H \bot B'C'\) \( \Rightarrow B'C' \bot \left( {AA'H} \right) \Rightarrow B'C' \bot AA'\).
Mà \(BB'//AA'\) nên \(B'C' \bot BB'\) hay \(BCC'B'\) là hình chữ nhật.
b) Tam giác \(AA'H\) vuông tại \(H\), ta có:\(A'H = \frac{{a\sqrt 3 }}{2} \Rightarrow AH = \sqrt {A{A^{{\rm{'}}2}} - A'{H^2}} = \frac{{3a}}{2}\).
Thể tích khối lăng trụ \(ABC \cdot A'B'C'\) bằng \({S_{A'B'C'}} \cdot AH = \frac{{3{a^3}\sqrt 3 }}{8}\).
c) Vì \(A'H\) là hình chiếu vuông góc của \(AA'\) trên mặt phẳng \(\left( {A'B'C'} \right)\) nên góc giữa đường thẳng \(AA'\) và mặt phẳng \(\left( {A'B'C'} \right)\) là góc giữa hai đường thẳng \(AA'\) và \(A'H\), mà \(\left( {AA',A'H} \right) = \widehat {AA'H}\).
Tam giác \(AA'H\) vuông tại \(H\), ta có: \({\rm{cos}}\widehat {AA'H} = \frac{{A'H}}{{AA'}} = \frac{1}{2} \Rightarrow \widehat {AA'H} = {60^ \circ }\).
Vậy góc giữa đường thẳng \(AA'\) và mặt phẳng \(\left( {A'B'C'} \right)\) bằng \({60^ \circ }\).