Giải bài 43 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = a,AA' = 2a\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(BB'\) và \(CC'\).
Đề bài
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = a,AA' = 2a\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(BB'\) và \(CC'\).
a) Tính theo a thể tích khối tứ diện \(AA'MN\).
b) Tính côsin góc nhị diện \(\left[ {A,MN,A'} \right]\).
Phương pháp giải - Xem chi tiết
a) Nhận xét \({S_{{\rm{AA'MN}}}} = \frac{1}{2}{S_{ABB'A'}} = {a^{}}\)và \(CC'\) song song với \(\left( {ABB'A'} \right)\) nên \({\rm{d}}\left( {N,\left( {AA'M} \right)} \right) = d\left( {C,\left( {ABB'A'} \right)} \right) = CH = \frac{{a\sqrt 3 }}{2}\)
Tính thể tích khối chóp \(AA'MN\) bằng \(\frac{1}{3} \cdot {S_{AA'M}} \cdot d\left( {N,\left( {AA'M} \right)} \right)\)
b. Gọi là trung điểm của \(MN\) thì\(\;AI\; \bot MN,A'I \bot MN \Rightarrow \left[ {A,MN,A'} \right] = \widehat {AIA'}\)
Tính \(AI,A'I\)
Áp dụng định lí côsin áp dụng cho tam giác \(AA'I\), ta có:\(\cos \widehat {AIA'} = \frac{{A{I^2} + A'{I^2} - A{A^{'2}}}}{{2 \cdot AI \cdot A'I}}\).
Lời giải chi tiết
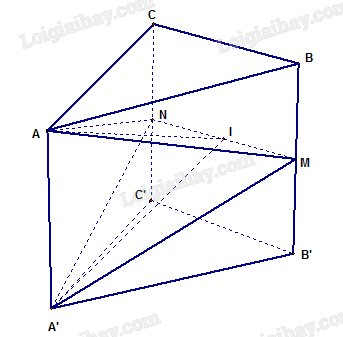
Ta có \({S_{{\rm{AA'MN}}}} = \frac{1}{2}{S_{ABB'A'}} = {a^{}}\)và \(CC'\) song song với \(\left( {ABB'A'} \right)\) nên \({\rm{d}}\left( {N,\left( {AA'M} \right)} \right) = d\left( {C,\left( {ABB'A'} \right)} \right) = CH = \frac{{a\sqrt 3 }}{2}\)
Thể tích khối chóp \(AA'MN\) bằng \(\frac{1}{3} \cdot {S_{AA'M}} \cdot d\left( {N,\left( {AA'M} \right)} \right) = \frac{{{a^3}\sqrt 3 }}{6}\)
b. Gọi là trung điểm của \(MN\) thì\(\;AI\; \bot MN,A'I \bot MN \Rightarrow \left[ {A,MN,A'} \right] = \widehat {AIA'}\)
\(AI = A'I = \sqrt {A{M^2} - M{I^2}} = \sqrt {A{B^2} + B{M^2} - M{I^2}} = \frac{{a\sqrt 7 }}{2}\)
Theo đinh lí côsin áp dụng cho tam giác \(AA'I\), ta có:
\(\cos \widehat {AIA'} = \frac{{A{I^2} + A'{I^2} - A{A^{'2}}}}{{2 \cdot AI \cdot A'I}} = \frac{{ - 1}}{7}\).