Giải bài 49 trang 110 sách bài tập toán 11 - Cánh diều
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình vuông cạnh \(a\)
Đề bài
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình vuông cạnh \(a\), \(AC\) cắt \(BD\) tại \(O\), \(SO \bot \left( {ABCD} \right)\), \(SA = 2a\). Tính khoảng cách:
a) Từ điểm \(A\) đến mặt phẳng \(\left( {SBD} \right)\).
b) Giữa hai đường thẳng \(SO\) và \(CD\).
c) Từ điểm \(O\) đến mặt phẳng \(\left( {SCD} \right)\).
d*) Giữa hai đường thẳng \(AB\) và \(SD\).
Phương pháp giải - Xem chi tiết
a) Chỉ ra rằng \(AO \bot \left( {SBD} \right)\), từ đó suy ra rằng khoảng cách cần tìm là đoạn thẳng \(AO\).
b) Gọi \(M\) là hình chiếu của \(O\) trên \(CD\). Chứng minh rằng \(OM\) là đường vuông góc chung của 2 đường thẳng \(SO\) và \(CD\), từ đó khoảng cách cần tìm là đoạn thẳng \(OM\).
c) Gọi \(H\) là hình chiếu của \(O\) trên \(SM\). Chứng minh rằng \(H\) cũng là hình chiếu của \(O\) trên \(\left( {SCD} \right)\), từ đó suy ra khoảng cách cần tìm là đoạn thẳng \(OH\).
d) Gọi \(G\) là hình chiếu của \(A\) trên \(\left( {SCD} \right)\). Chỉ ra rằng \(AB\parallel \left( {SCD} \right)\) và \(SD \subset \left( {SCD} \right)\) nên khoảng cách giữa \(AB\) và \(SD\) cũng chính là khoảng cách giữa \(AB\) và \(\left( {SCD} \right)\), và bằng \(AG\). Sử dụng định lí Thales để tính \(AG\).
Lời giải chi tiết
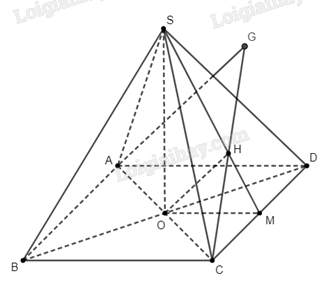
a) Ta có \(ABCD\) là hình vuông, nên \(AO \bot BD\). Hơn nữa, do \(SO \bot \left( {ABCD} \right)\) nên \(SO \bot AO\). Như vậy, do \(AO \bot BD\), \(SO \bot AO\) nên \(AO \bot \left( {SBD} \right)\). Điều này có nghĩa \(O\) là hình chiếu của \(A\) trên \(\left( {SBD} \right)\). Vậy khoảng cách từ \(A\) đến \(\left( {SBD} \right)\) là đoạn thẳng \(AO\).
Ta có \(ABCD\) là hình vuông cạnh \(a\), nên \(AC = a\sqrt 2 \Rightarrow AO = \frac{{a\sqrt 2 }}{2}\).
Vậy khoảng cách từ \(A\) đến \(\left( {SBD} \right)\) là \(\frac{{a\sqrt 2 }}{2}\).
b) Gọi \(M\) là hình chiếu của \(O\) trên \(CD\). Do \(O\) là tâm của hình vuông \(ABCD\) cạnh \(a\), nên ta suy ra \(OM \bot CD\) và \(OM = \frac{a}{2}\).
Do \(SO \bot \left( {ABCD} \right)\), ta suy ra \(SO \bot OM\).
Như vậy, do \(OM \bot CD\), \(SO \bot OM\), nên \(OM\) là đường vuông góc chung của 2 đường thẳng \(SO\) và \(CD\), điều này có nghĩa khoảng cách giữa 2 đường thẳng \(SO\) và \(CD\) là đoạn thẳng \(OM\).
Do \(OM = \frac{a}{2}\), ta kết luận rằng khoảng cách giữa 2 đường thẳng \(SO\) và \(CD\) là \(\frac{a}{2}\).
c) Gọi \(H\) là hình chiếu của \(O\) trên \(SM\). Vì \(SO \bot \left( {ABCD} \right)\) nên \(SO \bot CD\), mà \(OM \bot CD\) nên \(\left( {SOM} \right) \bot CD\), điều này suy ra \(OH \bot CD\). Mà lại có \(OH \bot SM\) nên \(OH \bot \left( {SCD} \right)\).
Vậy \(H\) là hình chiếu của \(O\) trên \(\left( {SCD} \right)\), tức là khoảng cách từ \(O\) đến \(\left( {SCD} \right)\) là đoạn thẳng \(OH\).
Tam giác \(SAO\) vuông tại \(O\) nên \(S{O^2} = S{A^2} - A{O^2} = {\left( {2a} \right)^2} - {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} = \frac{{7{a^2}}}{2}\).
Tam giác \(SOM\) vuông tại \(O\) có đường cao \(OH\), nên ta có:
\(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{M^2}}} = \frac{2}{{7{a^2}}} + \frac{4}{{{a^2}}} = \frac{{30}}{{7{a^2}}} \Rightarrow OH = \sqrt {\frac{{7{a^2}}}{{30}}} = \frac{{a\sqrt {210} }}{{30}}\).
d) Gọi \(G\) là hình chiếu của \(A\) trên \(\left( {SCD} \right)\).
Ta có \(AB\parallel CD\) nên \(AB\parallel \left( {SCD} \right)\), mà \(SD \subset \left( {SCD} \right)\), nên khoảng cách giữa 2 đường thẳng \(AB\) và \(SD\) cũng bằng khoảng cách giữa \(AB\) và \(\left( {SCD} \right)\), và bằng khoảng cách từ \(A\) đến \(\left( {SCD} \right)\). Do \(G\) là hình chiếu của \(A\) trên \(\left( {SCD} \right)\), nên khoảng cách cần tìm là đoạn thẳng \(AG\).
Do \(OH \bot \left( {SCD} \right)\), \(AG \bot \left( {SCD} \right)\) nên \(OH\parallel AG\).
Tam giác \(ACG\) có \(OH\parallel AG\), nên theo định lí Thales ta có \(\frac{{OH}}{{AG}} = \frac{{CO}}{{CA}} = \frac{1}{2}\).
Suy ra \(AG = 2OH\). Mà \(OH = \frac{{a\sqrt {210} }}{{30}}\) nên \(AG = \frac{{a\sqrt {210} }}{{15}}\).