Giải bài 5 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo
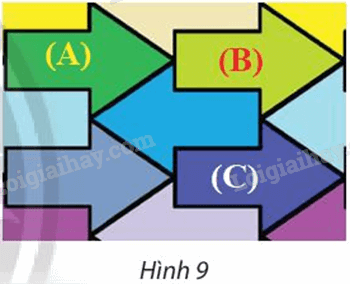
Trong Hình 9, tìm các vectơ \(\vec u\) và \(\vec v\) sao cho phép tịnh tiến \({T_{\vec u}}\)biến hình mũi tên (A) thành hình mũi tên (B) và phép tịnh tiến \({T_{\vec v}}\) biến hình mũi tên (A) thành hình mũi tên (C).
Đề bài
Trong Hình 9, tìm các vectơ \(\vec u\) và \(\vec v\) sao cho phép tịnh tiến \({T_{\vec u}}\) biến hình mũi tên (A) thành hình mũi tên (B) và phép tịnh tiến \({T_{\vec v}}\) biến hình mũi tên (A) thành hình mũi tên (C).
Phương pháp giải - Xem chi tiết
Quan sát hình 9 để làm
Lời giải chi tiết
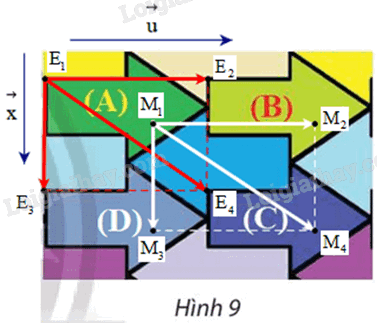
+ Gọi \({E_1}\) là một điểm trên hình mũi tên (A) và \(\vec u\) có phương song song với trục đối xứng của hình mũi tên (A), độ dài bằng độ dài từ điểm đầu tới điểm cuối của mũi tên (A) (hình vẽ).
Lấy điểm \({E_2}\;\) sao cho \(\overrightarrow {{E_1}{E_2}} = \vec u\)
Khi đó \({E_2}\;\) là một điểm trên hình mũi tên (B) có vị trí tương ứng với điểm \({E_1}\) trên hình mũi tên (A).
Tương tự như vậy, với mỗi điểm \({M_1}\) bất kì trên hình mũi tên (A), ta lấy điểm \({M_2}\) sao cho \(\overrightarrow {{M_1}{M_2}} = \vec u\) thì ta được tập hợp các điểm \({M_2}\) tạo thành hình mũi tên (B).
Do đó phép tịnh tiến theo \(\vec u\) biến hình mũi tên (A) thành hình mũi tên (B).
+ Ta gọi (D) là hình mũi tên nằm bên dưới hình mũi tên (A) và bên trái hình mũi tên (C) (như hình vẽ).
Gọi \({E_3}\) là một điểm trên hình mũi tên (D) có vị trí tương ứng với điểm E 1 trên hình mũi tên (A).
Giả sử \(\vec x\) là vectơ có phương vuông góc với trục đối xứng của hình mũi tên (A), độ dài bằng độ dài từ điểm E 1 đến điểm E 3 (hình vẽ).
Tức là, \(\vec x = \overrightarrow {{E_1}{E_3}} \)
Lấy điểm \({E_4}\) sao cho tứ giác \({E_1}{E_2}{E_4}{E_3}\;\) là hình bình hành.
Áp dụng quy tắc hình bình hành, ta được \(\overrightarrow {{E_1}{E_4}} = \overrightarrow {{E_1}{E_2}} + \overrightarrow {{E_1}{E_3}} = \vec u + \vec x\).
Lúc này, ta thấy \({E_4}\) là một điểm trên hình mũi tên (C) có vị trí tương ứng với điểm \({E_1}\) trên hình mũi tên (A).
Tương tự như vậy, với mỗi điểm \({M_1}\) bất kì trên hình mũi tên (A), ta lấy điểm \({M_4}\) sao cho \(\overrightarrow {{M_1}{M_4}} = \vec u + \vec x\) thì ta được tập hợp các điểm M 4 tạo thành hình mũi tên (C).
Do đó phép tịnh tiến theo \(\vec v = \vec u + \vec x\) biến hình mũi tên (A) thành hình mũi tên (C).