Giải bài 5 trang 76 sách bài tập toán 10 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Một tháp làm nguội của một nhà máy có mặt cát là hình hypebol có phương trình $\frac{{{x^2}}}{{30}} - \frac{{{y^2}}}{{50}} = 1$. Biết chiều cao của tháp là 120 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng $\frac{1}{2}$ khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính đáy của tháp.

Lời giải chi tiết

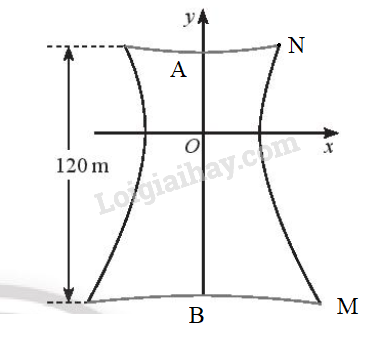
Ta có: O(0;0) là tâm đối xứng của hypebol

=> khoảng cách từ nóc tháp đến tâm đối xứng là OA, khoảng cách từ tâm đối xứng đến đáy là OB và $OA = \frac{1}{2}OB$

Mà chiều cao tháp là 120m hay $OA + OB = 120$$\Rightarrow OA = 40(m);OB = 80(m)$

Gọi r và R lần lượt là bán kính nóc và bán kính đáy của tháp.

Lấy N là điểm trên nóc tháp, thuộc vào hypebol $\Rightarrow N\left( {r;40} \right)$

Tương tự,  M là điểm ở đáy tháp, thuộc vào hypebol $\Rightarrow M\left( {R; - 80} \right)$

Thay tọa độ điểm $M\left( {R; - 80} \right),N\left( {r;40} \right)$ vào phương trình hypebol ta tính được:

$R = 30\sqrt {1 + \frac{{{{\left( { - 80} \right)}^2}}}{{{{50}^2}}}}  \approx 57\left( m \right),r = 30\sqrt {1 + \frac{{{{40}^2}}}{{{{50}^2}}}}  \approx 38\left( m \right)$

Vậy bán kính nóc là 38m, bán kính đáy là 57m.