Giải bài 5 trang 99 sách bài tập toán 9 - Chân trời sáng tạo tập 1
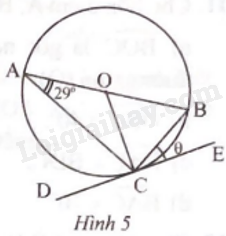
Cho biết DE là tiếp tuyến của đường tròn trong Hình 5. Số đo (theta ) của góc (widehat {BCE}) trong hình là A. 29o B. 61o C. 58o D. 32o
Đề bài
Cho biết DE là tiếp tuyến của đường tròn trong Hình 5. Số đo \(\theta \) của góc \(\widehat {BCE}\) trong hình là
A. 29 o
B. 61 o
C. 58 o
D. 32 o
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức về tiếp tuyến và góc nội tiếp chắn nửa đường tròn.
Lời giải chi tiết
Tam giác OAC có OA = OC = R nên \(\widehat {OAC} = \widehat {OCA} = 29^\circ\)
Tam giác ABC có \(\widehat{ACB} = 90^\circ\) (góc nội tiếp chắn nửa đường tròn).
DE là tiếp tuyến của đường tròn nên \(OC \bot CE\) hay \(\widehat{OCE} = 90^\circ\)
Suy ra \(\widehat{ACB} = \widehat{OCE}\)
hay \(\widehat{OCA} + \widehat{OCB} = \widehat{OCB} + \widehat{BCE}\)
suy ra \(\widehat{OCA} = \widehat{BCE} = 29^\circ\)
Chọn đáp án A.