Giải bài 6. 10 trang 9 sách bài tập toán 10 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

Có hai địa điểm A, B cùng nằm trên một tuyến quốc lộ thẳng. Khoảng cách giữa A và B là 20 km. Một xe máy xuất phát từ A lúc 6 giờ và chạy với vận tốc 40 km/h theo chiều từ A đến B. Một ô tô xuất phát từ B lúc 8 giờ và chạy với vận tốc 80 km/h theo cùng chiều với xe máy. Coi chuyển động của xe máy và ô tô là thẳng đều. Chọn A làm mốc, chọn thời điểm 6 giờ làm mốc thời gian và chọn chiều từ A đến B làm chiều dương. Khi đó tọa độ của xe máy và ô tô sẽ là những hàm số của biến thời gian.

a) Viết PT chuyển động của xe máy và ô tô (tức là công thức hàm tọa độ theo thời gian)

b) Vẽ đồ thị hàm tọa độ của xe máy và ô tô trên cùng một hệ trục tọa độ

c) Căn cứ vào đồ thị vẽ được, hãy xác định vị trí và thời điểm ô tô đuổi kịp xe máy

d) Kiểm tra lại kết quả tìm được ở câu c) bằng cách giải các phương trình chuyển động của xe máy và ô tô.

Lời giải chi tiết

a) Gọi t ( t > 0) là thời gian chuyển động của xe máy

Quãng đường xe máy đi được là: S ₁ = 40 t (km)

Quãng đường ô tô đi được là: S ₂ = AB + 80(t – 2) = 80t – 140 (km)

\( \Rightarrow \) Phương trình chuyển động của xe máy là: \(y = {S_1}(t) = 40t\), của ô tô là: \(y = {S_2}(t) = 80t - 140\)

b) Ta có đồ thị

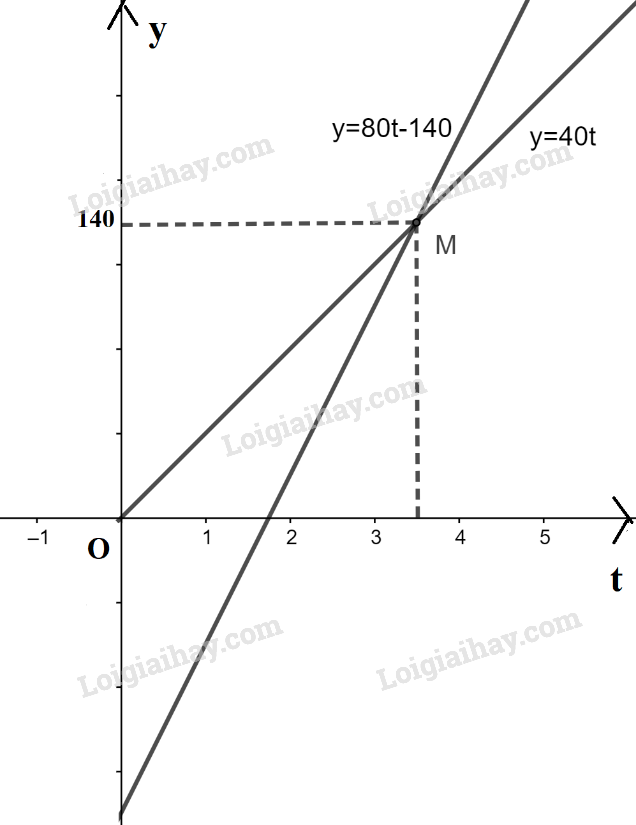
c) Từ đồ thị ta thấy 2 đồ thị cắt nhau tại điểm \(M\left( {\frac{7}{2};140} \right)\). Như vậy ô tô đuổi kịp xe máy lúc 9h 30 phút tại vị trí cách A 140 km

d) Xét PT hoành độ: \(40t = 80t - 140 \Leftrightarrow t = \frac{7}{2}\)

Với \(t = \frac{7}{2}\) thì y = 140. Vậy ô tô đuổi kịp xe máy lúc 9h 30 phút tại vị trí cách A 140 km