Giải bài 6 trang 76 SGK Toán 8 tập 2– Chân trời sáng tạo — Không quảng cáo

Đề bài

Một người đo chiều cao của một tòa nhà nhờ một cọc chôn xuống đất, cọc cao 3m và đặt cách xa tòa nhà 27m. Sau khi người ấy lùi xa cái cọc 1,2m thì nhìn thấy đầu cọc và đỉnh tòa nhà cùng năm trên một đường thẳng. Hỏi tòa nhà cao bao nhiêu mét, biết rằng khoảng cách từ chân đến mắt người ấy là 1,5m.

Lời giải chi tiết

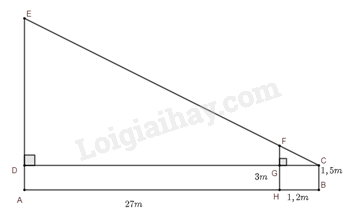
Giả sử, ta biểu diễn người quan sát, cái cọc, tòa nhà có dạng như hình vẽ.

Chiều cao người quan sát là \(CB = 1,5m\); chiều cao cái cọc là \(HF = 3m\); khoảng cách từ người đến cọc là \(HB = 1,2m\); khoảng cách từ tòa nhà đến cọc là \(AH = 27m\). Chiều cao tòa nhà là \(AE\).

Vì tứ giác \(GHBC\) là hình chữ nhật nên \(GC = HB = 1,2m\); Vì tứ giác \(GHAD\) là hình chữ nhật nên \(AH = DG = 27m;GH = AD = 1,5m\).

Chiều dài đoạn \(CD\) là: \(DC = DG + GC = 27 + 1,2 = 28,2m\).

Độ dài đoạn \(GF\) là: \(GF = FH - GH = 3 - 1,5 = 1,5m\)

Xét \(\Delta DEC\) và \(\Delta GFC\) có:

\(\widehat C\) chung

\(\widehat {EDC} = \widehat {FGC} = 90^\circ \)

Do đó, \(\Delta DEC\backsim\Delta GFC\) (g.g)

Vì \(\Delta DEC\backsim\Delta GFC\) nên \(\frac{{DC}}{{GC}} = \frac{{DE}}{{GF}}\) (các cặp cạnh tương ứng)

Thay số, \(\frac{{28,2}}{{1,2}} = \frac{{DE}}{{1,5}} \Rightarrow DE = \frac{{28,2.1,5}}{{1,2}} = 35,25m\)

Chiều cao của tòa nhà là:

\(AD + DE = 35,25 + 1,5 = 36,75m\)

Vậy chiều cao tòa nhà là 36,75m.