Giải bài 7.46 trang 36 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Cho hàm số \(y = \left( {2m - 1} \right)x + 5\left( {m \ne \frac{1}{2}} \right)\)
Đề bài
Cho hàm số \(y = \left( {2m - 1} \right)x + 5\left( {m \ne \frac{1}{2}} \right)\)
a) Tìm m để đồ thị hàm số song song với đường thẳng \(y = - 3x\)
b) Vẽ đồ thị hàm số với giá trị m vừa tìm được ở câu a.
c) Tìm giao điểm A của đồ thị hàm số ở câu b và đồ thị của hàm số \(y = x + 5\). Tính diện tích của tam giác OAB, trong đó B là giao điểm của đồ thị hàm số \(y = x + 5\) với trục Ox.
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức vị trí tương đối của hai đường thẳng để tìm m:
Cho hai đường thẳng \(\left( d \right):y = ax + b\left( {a \ne 0} \right)\,\) và \(\left( {d'} \right):y = a'x + b'\left( {a' \ne 0} \right)\,\). Khi đó, d song song với d’ nếu \(a = a',b \ne b'\)
b) Sử dụng kiến thức về cách vẽ đồ thị hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\) để vẽ đồ thị:
+ Khi \(b = 0\) thì \(y = ax\). Đồ thị của hàm số \(y = ax\) là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a)
+ Khi \(b \ne 0\), ta thường xác định hai điểm đặc biệt trên đồ thị là giao điểm của đồ thị với hai trục tọa độ như sau:
- Cho \(x = 0\) thì \(y = b\), ta được điểm P(0; b) thuộc trục tung Oy.
- Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( { - \frac{b}{a};0} \right)\) thuộc trục hoành Ox.
- Vẽ đường thẳng đi qua hai điểm P, Q ta được đồ thị của hàm số \(y = ax + b\)
c) + Tìm tọa độ giao điểm của hai đường thẳng theo các bước:
Bước 1: Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2: Thay hoành độ giao điểm vừa tìm được vào một trong hai hàm số ta tìm được tung độ giao điểm.
+ Tam giác OAB vuông tại O nên diện tích tam giác AOB là: \(S = \frac{1}{2}OA.OB\)
Lời giải chi tiết
a) Vì đồ thị hàm số \(y = \left( {2m - 1} \right)x + 5\) song song với đường thẳng \(y = - 3x\) nên \(2m - 1 = - 3\)
\(2m = - 2\), suy ra\(m = - 1\) (thỏa mãn)
b) Với \(m = - 1\) ta có: \(y = - 3x + 5\)
Đồ thị hàm số \(y = - 3x + 5\) đi qua hai điểm \(D\left( {0;5} \right),C\left( {\frac{5}{3};0} \right)\)
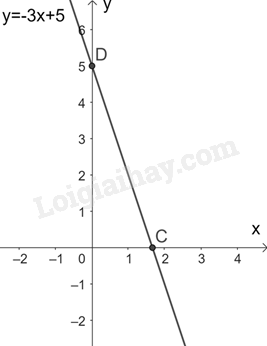
c) Hoành độ giao điểm của hai đồ thị hàm số \(y = x + 5\) và \(y = - 3x + 5\) là nghiệm của phương trình: \(x + 5 = - 3x + 5\)
\(x = 0\) nên \(y = 5\)
Do đó, điểm \(A\left( {0;5} \right)\)
Vì B là giao điểm của đồ thị hàm số \(y = x + 5\) với trục Ox nên \(x + 5 = 0\), suy ra \(x = - 5\)
Do đó, \(B\left( { - 5;0} \right)\)
Vì tam giác OAB vuông tại O nên diện tích tam giác OAB là: \(\frac{1}{2}OA.OB = \frac{1}{2}.5.\left| { - 5} \right| = \frac{{25}}{2}\)