Giải bài 7 trang 100, 101 vở thực hành Toán 9 tập 2
Cho hình vuông ABCD nội tiếp (O) với (AB = 4cm). Hãy tính diện tích hình viên phân giới hạn bởi dây cung AB và cung nhỏ AB của (O).
Đề bài
Cho hình vuông ABCD nội tiếp (O) với \(AB = 4cm\). Hãy tính diện tích hình viên phân giới hạn bởi dây cung AB và cung nhỏ AB của (O).
Phương pháp giải - Xem chi tiết
Theo định lí Pythagore tính được AC, từ đó tính được bán kính R của (O).
+ Hình tròn tâm O bán kính R có diện tích là \({S_1} = \pi {R^2}\).
+ Hình vuông ABCD có diện tích là \({S_2} = A{B^2}\).
+ Vì bốn cạnh AB, BC, CD, DA của hình vuông lần lượt cùng với bốn cung nhỏ AB, BC, CD, DA giới hạn bốn hình viên phân bằng nhau nên mỗi hình này có diện tích là \(S = \frac{1}{4}\left( {{S_1} - {S_2}} \right)\)
Lời giải chi tiết
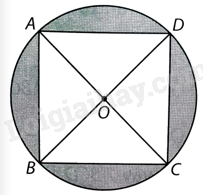
Theo định lí Pythagore, ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {16 + 16} = 4\sqrt 2 \left( {cm} \right)\).
Vậy đường tròn (O) có bán kính:
\(R = \frac{{AC}}{2} = 2\sqrt 2 \left( {cm} \right)\).
Hình tròn tâm O bán kính R có diện tích là \({S_1} = \pi {R^2} = 8\pi \left( {c{m^2}} \right)\).
Hình vuông ABCD có diện tích là \({S_2} = A{B^2} = 16\left( {c{m^2}} \right)\).
Vì bốn cạnh AB, BC, CD, DA của hình vuông lần lượt cùng với bốn cung nhỏ AB, BC, CD, DA giới hạn bốn hình viên phân bằng nhau nên mỗi hình này có diện tích là:
\(S = \frac{1}{4}\left( {{S_1} - {S_2}} \right) = \left( {2\pi - 4} \right)\left( {c{m^2}} \right)\).