Giải bài 7 trang 60 sách bài tập toán 8 – Cánh diều
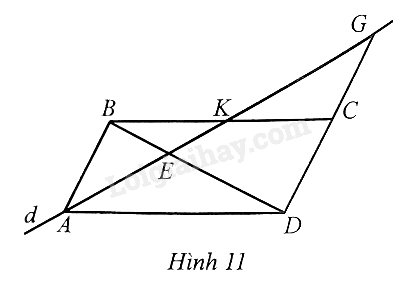
Cho \(ABCD\) là hình bình hành. Một đường thẳng \(d\) đi qua \(A\) cắt \(BD,BC,DC\) lần lượt tại \(E,K,G\) (Hình 11). Chứng minh:
Đề bài
Cho \(ABCD\) là hình bình hành. Một đường thẳng \(d\) đi qua \(A\) cắt \(BD,BC,DC\) lần lượt tại \(E,K,G\) (Hình 11). Chứng minh:
a) \(A{E^2} = EK.EG\)
b) \(\frac{1}{{AE}} = \frac{1}{{AK}} + \frac{1}{{AG}}\)
Phương pháp giải - Xem chi tiết
Hệ quả của định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết
a) Do \(AD//BK,AB//DG\) nên theo hệ quả của định lí Thales, ta có:
\(\frac{{EK}}{{AE}} = \frac{{EB}}{{ED}} = \frac{{AE}}{{EG}}\) hay \(\frac{{EK}}{{AE}} = \frac{{AE}}{{EG}}\)
→ \(A{E^2} = EK.EG\).
b) Ta có:
\(\frac{{AE}}{{AK}} = \frac{{DE}}{{DB}};\frac{{AE}}{{AG}} = \frac{{BE}}{{BD}}\)
Nên \(\frac{{AE}}{{AK}} + \frac{{AE}}{{AG}} = \frac{{DE}}{{DB}} + \frac{{BE}}{{BD}} = \frac{{BD}}{{BD}} = 1\)
→ \(AE.\left( {\frac{1}{{AK}} + \frac{1}{{AG}}} \right) = 1\)
Vậy \(\frac{1}{{AE}} = \frac{1}{{AK}} = \frac{1}{{AG}}\).