Giải bài 7 trang 90 sách bài tập toán 8 - Cánh diều
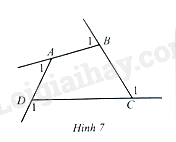
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác. Chứng minh tổng các góc ngoài của tứ giác \(ABCD\) ở Hình 7 (tại mỗi đỉnh chỉ nhọn một góc ngoài):
Đề bài
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác. Chứng minh tổng các góc ngoài của tứ giác \(ABCD\) ở Hình 7 (tại mỗi đỉnh chỉ nhọn một góc ngoài):
\(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 360^\circ \).
Phương pháp giải - Xem chi tiết
Dựa vào tính chất tổng các góc trong một tứ giác bằng \(360^\circ \) để chứng minh.
Lời giải chi tiết
Trong tứ giác \(ABCD\), ta có: \(\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {CDA} = 360^\circ \)
Ta có: \(\widehat {DAB} + \widehat {{A_1}} = \widehat {ABC} + \widehat {{B_1}} = \widehat {BCD} + \widehat {{C_1}} = \widehat {CDA} + \widehat {{D_1}} = 180^\circ \) (các cặp góc kề bù)
Suy ra \(\left( {180^\circ - \widehat {{A_1}}} \right) + \left( {180^\circ - \widehat {{B_1}}} \right) + \left( {180^\circ - \widehat {{C_1}}} \right) + \left( {180^\circ - \widehat {{D_1}}} \right) = 360^\circ \)
Hay \(720^\circ - \left( {\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}} \right) = 360^\circ \). Vậy \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 360^\circ \).