Giải bài 7 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Một người ngồi trên trạm quan sát cao 15 m so với mực nước biển. Vào ngày trời trong xanh thì tầm nhìn xa tối đa của người đó là bao nhiêu kilomet? Biết rằng bán kính Trái Đất là khoảng 6400 km. Làm tròn kết quả đến hàng phần trăm.
Đề bài
Một người ngồi trên trạm quan sát cao 15 m so với mực nước biển. Vào ngày trời trong xanh thì tầm nhìn xa tối đa của người đó là bao nhiêu kilomet? Biết rằng bán kính Trái Đất là khoảng 6400 km. Làm tròn kết quả đến hàng phần trăm.

Phương pháp giải - Xem chi tiết
Dựa vào: Một đường thẳng là tiếp tuyến của đường tròn khi nó đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó.
Vận dụng định lý Pytago.
Lời giải chi tiết
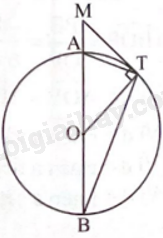
Theo đề bài ta có hình vẽ trên. Trong đó điểm M biểu diễn vị trí của người ngồi trên trạm quan sát, điểm A biểu diễn vị trí của trạm quan sát, điểm T biểu diễn điểm xa nhất mà người đó nhìn thấy. Khi đó đoạn thẳng MT gọi là tầm nhìn xa tối đa từ M.
Vì T là điểm nhìn xa tối đa nên MT là tiếp tuyến của đường tròn (đường tròn coi như bề mặt Trái Đất). Đặt h = MA = 15 m, R = OA = OT = 6400 km.
Áp dụng định lý Pytago vào tam giác OTM vuông tại T, ta có:
\(M{T^2} = O{M^2} - O{T^2} = {(h + R)^2} - {R^2} = {h^2} + 2Rh\)
Suy ra MT = \(\sqrt {{h^2} + 2Rh} = \sqrt {{{0,015}^2} + 2.6400.0,015} \approx 13,86(km)\)
Vậy tầm nhìn xa tối đa của người đó là 13,86 km.