Giải bài 8.1 trang 43 sách bài tập toán 9 - Kết nối tri thức tập 2
Túi I có hai viên bi màu đen, kí hiệu là ({B_1},{B_2}) và 2 viên bi màu trắng, kí hiệu là ({T_1},{T_2}). Túi II có 3 viên bi màu xanh, kí hiệu là ({X_1},{X_2},{X_3}) và 2 viên bi màu đỏ, kí hiệu là ({D_1},{D_2}), các viên bi có cùng kích thước. Từ mỗi túi lấy ngẫu nhiên một viên bi. a) Phép thử là gì? b) Mô tả không gian mẫu của phép thử.
Đề bài
Túi I có hai viên bi màu đen, kí hiệu là \({B_1},{B_2}\) và 2 viên bi màu trắng, kí hiệu là \({T_1},{T_2}\). Túi II có 3 viên bi màu xanh, kí hiệu là \({X_1},{X_2},{X_3}\) và 2 viên bi màu đỏ, kí hiệu là \({D_1},{D_2}\), các viên bi có cùng kích thước. Từ mỗi túi lấy ngẫu nhiên một viên bi.
a) Phép thử là gì?
b) Mô tả không gian mẫu của phép thử.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về phép thử để tìm phép thử: Một hoặc một số hành động, thực nghiệm được tiến hành liên tiếp hay đồng thời mà kết quả của chúng không thể biết được trước khi thực hiện nhưng có thể liệt kê các kết quả có thể xảy ra, được gọi là một phép thử ngẫu nhiên, gọi tắt là phép thử.
Sử dụng kiến thức về không gian mẫu để tìm không gian mẫu: Sử dụng kiến thức về không gian mẫu để tìm không gian mẫu: Tập hợp tất cả các kết quả có thể xảy ra của phép thử (gọi tắt là tập tất cả các kết quả có thể của phép thử) được gọi là không gian mẫu của phép thử.
Lời giải chi tiết
a) Phép thử là lấy ngẫu nhiên một viên bi từ mỗi túi.
b) Kết quả của phép thử là (a, b) trong đó a và b tương ứng là màu quả bóng lấy ra ở túi I và túi II.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng:
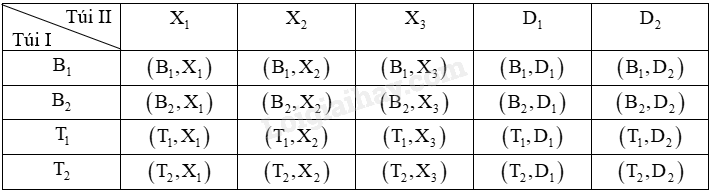
Mỗi ô trong bảng là một kết quả có thể. Không gian mẫu là tập hợp 20 ô của bảng trên.
Vậy \(\Omega = \{\left( {{B_1},{X_1}} \right); \left( {{B_2},{X_1}} \right); \left( {{T_1},{X_1}} \right); \left( {{T_2},{X_1}} \right);\\ \left( {{B_1},{X_2}} \right); \left( {{B_2},{X_2}} \right); \left( {{T_1},{X_2}} \right); \left( {{T_2},{X_2}} \right);\\ \left( {{B_1},{X_3}} \right); \left( {{B_2},{X_3}} \right); \left( {{T_1},{X_3}} \right); \left( {{T_2},{X_3}} \right); \\\left( {{B_1},{D_1}} \right); \left( {{B_2},{D_1}} \right); \left( {{T_1},{D_1}} \right); \left( {{T_2},{D_1}} \right);\\ \left( {{B_1},{D_2}} \right); \left( {{B_2},{D_2}} \right); \left( {{T_1},{D_2}} \right); \left( {{T_2},{D_2}} \right)\}\)