Giải bài 8 trang 82 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Từ điểm A nằm ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B, C là tiếp điểm). Kẻ đường kính CD của đường tròn (O), đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là M. Gọi H là giao điểm của AO và BC. Chứng minh (widehat {AHC} = {90^o}) và tứ giác AMHC nội tiếp đường tròn.
Đề bài
Từ điểm A nằm ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B, C là tiếp điểm). Kẻ đường kính CD của đường tròn (O), đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là M. Gọi H là giao điểm của AO và BC. Chứng minh \(\widehat {AHC} = {90^o}\) và tứ giác AMHC nội tiếp đường tròn.
Phương pháp giải - Xem chi tiết
Chứng minh tam giác AMC và tam giác AHC nội tiếp đường tròn đường kính AC. Từ đó suy ra AMHC nội tiếp đường tròn.
Lời giải chi tiết
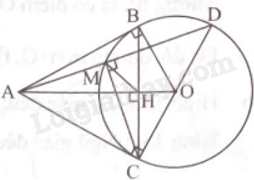
Ta có AB = AC (tính chất hai tiếp tuyến cắt nhau); OA = OB = R.
Suy ra OA là đường trung trực của đoạn thẳng BC, suy ra \(\widehat {AHC} = {90^o}\).
Ta có \(\widehat {CMD} = {90^o}\) (góc nội tiếp chắn nửa đường tròn), suy ra \(\widehat {AMC} = {90^o}\).
Tam giác AMC vuông tại M và tam giác AHC vuông tại H cùng nội tiếp đường tròn đường kính AC.
Do đó, tứ giác AMHC nội tiếp đường tròn đường kính AC.