Giải bài 9.47 trang 63 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Cho tam giác nhọn ABC có các đường cao AD, BE, CF cắt nhau ở H. Chứng minh rằng: a) (HA.HD = HB.HE = HC.HF);
Đề bài
Cho tam giác nhọn ABC có các đường cao AD, BE, CF cắt nhau ở H. Chứng minh rằng:
a) \(HA.HD = HB.HE = HC.HF\);
b) $\Delta AFC\backsim \Delta AEB$ và $AF.AB=AE.AC\,;$
c) $\Delta BDF\backsim \Delta EDC$ và DA là tia phân giác của góc EDF.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức trường hợp đồng dạng của tam giác vuông để chứng minh: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
+ Sử dụng kiến thức về trường hợp đồng dạng của tam giác để chứng minh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
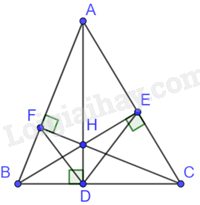
a) Vì AD, BE, CF là các đường cao của tam giác ABC nên \(AD \bot BC,BE \bot AC,CF \bot AB\)
nên \(\widehat {AEB} = \widehat {BEC} = \widehat {ADB} = \widehat {ADC} = \widehat {CFA} = \widehat {CFB} = {90^0}\)
Tam giác AHE và tam giác BHD có:
\(\widehat {AEH} = \widehat {HDB} = {90^0}\) (cmt), \(\widehat {AHE} = \widehat {BHD}\) (hai góc đối đỉnh). Do đó, $\Delta AHE\backsim \Delta BHD\left( g-g \right)$
Suy ra: \(\frac{{AH}}{{BH}} = \frac{{HE}}{{HD}}\) nên \(HA.HD = HB.HE\) (1)
Tam giác HBF và tam giác HCE có:
\(\widehat {HFB} = \widehat {HEC} = {90^0}\) (cmt), \(\widehat {BHF} = \widehat {EHC}\) (hai góc đối đỉnh). Do đó, $\Delta HBF\backsim \Delta HCE\left( g-g \right)$
Suy ra: \(\frac{{HB}}{{HC}} = \frac{{HF}}{{HE}}\) nên \(HB.HE = HC.HF\) (2)
Từ (1) và (2) ta có: \(HA.HD = HB.HE = HC.HF\)
b) Tam giác AFC và tam giác AEB có:
\(\widehat {AFC} = \widehat {AEC} = {90^0},\widehat {BAC}\;chung\)
Do đó, $\Delta AFC\backsim \Delta AEB\left( g-g \right)$
Suy ra: \(\frac{{AF}}{{AE}} = \frac{{AC}}{{AB}}\) nên \(AF.AB = AE.AC\,\)
c) Vì \(HA.HD = HB.HE\) nên \(\frac{{HA}}{{HE}} = \frac{{HB}}{{HD}}\)
Tam giác HAB và tam giác HED có: \(\frac{{HA}}{{HE}} = \frac{{HB}}{{HD}}\) (cmt), \(\widehat {AHB} = \widehat {HED}\) (hai góc đối đỉnh)
Do đó, $\Delta AHB\backsim \Delta EHD\left( c-g-c \right)$, suy ra: \(\widehat {HAB} = \widehat {HED}\)
Mà \(\widehat {HAB} + \widehat {FBD} = \widehat {HED} + \widehat {DEC}\left( { = {{90}^0}} \right)\)
Do đó, \(\widehat {FBD} = \widehat {DEC}\)
Chứng minh tương tự ta có: \(\widehat {BFD} = \widehat {ECD}\)
Tam giác BDF và tam giác EDC có: \(\widehat {FBD} = \widehat {DEC}\) (cmt), \(\widehat {BFD} = \widehat {ECD}\) (cmt). Do đó, $\Delta BDF\backsim \Delta EDC\left( g-g \right)$
Suy ra: \(\widehat {BDF} = \widehat {EDC}\)
Mà \(\widehat {BDF} + \widehat {FDH} = \widehat {EDC} + \widehat {HDE}\left( { = {{90}^0}} \right)\)
Do đó, \(\widehat {FDH} = \widehat {HDE}\)
Vậy DA là tia phân giác của góc EDF