Giải bài 9.49 trang 63 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Cho tam giác ABC vuông tại A có đường cao AH. Cho M là một điểm nằm trên cạnh BC (M nằm giữa C và H).
Đề bài
Cho tam giác ABC vuông tại A có đường cao AH. Cho M là một điểm nằm trên cạnh BC (M nằm giữa C và H). Kẻ đường thẳng qua M vuông góc với BC lần lượt cắt AC và tia đối của tia AB tại N và P. Chứng minh rằng:
a) $\Delta ANP\backsim \Delta HBA$ và $\Delta MCN\backsim \Delta MPB$;
b) \(\frac{{MB}}{{MC}}.\frac{{NC}}{{NA}}.\frac{{PA}}{{PB}} = 1\)
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc) để chứng minh tam giác đồng dạng: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
b) Sử dụng định lí Thalès để chứng minh: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
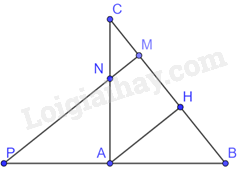
Vì tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^0}\)
Mà \(\widehat {BAC} + \widehat {PAN} = {180^0}\) (hai góc kề bù)
Do đó \(\widehat {PAN} = {90^0}\)
Vì \(AH \bot BC\) (do AH là đường cao của tam giác ABC) nên \(\widehat {AHB} = \widehat {AHC} = {90^0}\)
Vì \(MN \bot BC\) nên \(\widehat {NMC} = \widehat {NMB} = {90^0}\)
Vì \(MN \bot BC\), \(AH \bot BC\) nên MN//AH
Do đó, \(\widehat P = \widehat {HAB}\) (hai góc đồng vị)
Tam giác ANP và tam giác HBA có:
\(\widehat {NAP} = \widehat {AHB} = {90^0},\)\(\widehat P = \widehat {HAB}\) (cmt)
Do đó, $\Delta ANP\backsim \Delta HBA\left( g-g \right)$
Tam giác MCN và tam giác MPB có:
\(\widehat {NMC} = \widehat {NMB} = {90^0},\widehat C = \widehat P\) (cùng phụ với góc B)
Do đó, $\Delta MCN\backsim \Delta MPB\left( g-g \right)$
b) Ta có: \(\frac{{MB}}{{MC}}.\frac{{NC}}{{NA}}.\frac{{PA}}{{PB}} = \frac{{MB}}{{PB}}.\frac{{NC}}{{NA}}.\frac{{PA}}{{MC}}\)
Tam giác PMB có: PM//AH nên theo định lí Thalès ta có: \(\frac{{MB}}{{MH}} = \frac{{PB}}{{PA}}\), suy ra \(\frac{{MB}}{{PB}} = \frac{{MH}}{{PA}}\)
Tam giác AHC có: MN//AH nên theo định lí Thalès ta có: \(\frac{{NC}}{{NA}} = \frac{{MC}}{{MH}}\)
Do đó: \(\frac{{MB}}{{PB}}.\frac{{NC}}{{NA}}.\frac{{PA}}{{MC}} = \frac{{MH}}{{PA}}.\frac{{MC}}{{MH}}.\frac{{PA}}{{MC}} = 1\)