Giải bài 9.51 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác nhọn ABC có đường cao AH. Các điểm M và N lần lượt là hình chiếu vuông góc của H trên AB, AC. Chứng minh rằng (AM.AB = AN.AC).
Đề bài
Cho tam giác nhọn ABC có đường cao AH. Các điểm M và N lần lượt là hình chiếu vuông góc của H trên AB, AC. Chứng minh rằng \(AM.AB = AN.AC\).
Phương pháp giải - Xem chi tiết
+ Chứng minh tứ giác AMHN nội tiếp đường tròn đường kính AH, suy ra \(\widehat {AMN} = \widehat {AHN}\).
+ Ta có: \(\widehat {AMN} = \widehat {AHN} = {90^o} - \widehat {HAN} = \widehat {ACB}\).
+ Chứng minh $\Delta AMN\backsim \Delta ACB\left( g.g \right)$, suy ra \(AM.AB = AN.AC\).
Lời giải chi tiết
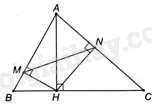
Vì \(\widehat {AMH} = \widehat {ANH} = {90^o}\) nên tam giác AMH vuông tại M và tam giác ANH vuông tại N.
Suy ra, hai tam giác AMH, ANH nội tiếp đường tròn đường kính AH.
Suy ra, tứ giác AMHN nội tiếp đường tròn đường kính AH.
Do đó, \(\widehat {AMN} = \widehat {AHN}\) (hai góc nội tiếp đường tròn đường kính AH cùng chắn cung AN).
Ta có: \(\widehat {AMN} = \widehat {AHN} = {90^o} - \widehat {HAN} = \widehat {ACB}\)
Tam giác AMN và tam giác ACB có:
\(\widehat {AMN} = \widehat {ACB}\) (cmt),
\(\widehat {MAN} = \widehat {CAB}\) (góc chung)
nên $\Delta AMN\backsim \Delta ACB\left( g.g \right)$.
Suy ra \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\), suy ra \(AM.AB = AN.AC\).