Giải bài 9 trang 120 SGK Toán 7 tập 2 - Cánh diều
Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt. Chứng minh rằng: a) Nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng; b) Nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.
Đề bài
Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt. Chứng minh rằng:
a) Nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng;
b) Nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.
Phương pháp giải - Xem chi tiết
a) Trong tam giác cân: đường trung tuyến tại đỉnh cân đồng thời là đường cao và đường phân giác của góc tại đỉnh đó.
b) Chứng minh tam giác ABC cân tại A , ta chứng minh AB = AC hoặc góc B bằng góc C .
Lời giải chi tiết
a)
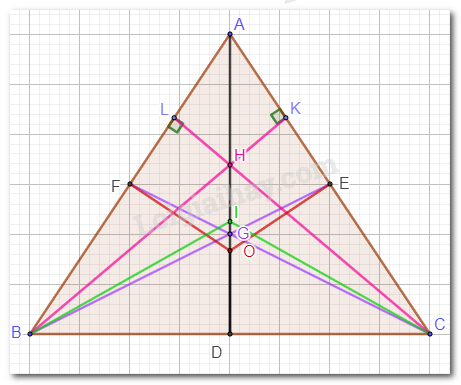
Trong tam giác ABC cân tại A có AD là đường trung tuyến.
Xét tam giác ABD và tam giác ACD có:
AB = AC (tam giác ABC cân);
AD chung;
BD = DC ( D là trung điểm của BC ).
Vậy \(\Delta ABD = \Delta ACD\)(c.c.c.). Suy ra: \(\widehat {ADB} = \widehat {ADC} = 90^\circ \) (vì ba điểm B, D, C thẳng hàng); \(\widehat {BAD} = \widehat {CAD}\).
Vậy AD là đường cao của tam giác và đường phân giác của góc A .
Suy ra: AD là đường trung trực của tam giác ABC .
Vậy AD là đường trung tuyến, đường cao, đường phân giác, đường trung trực của tam giác ABC .
Mà G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực nên A, G, H, I, O cùng nằm trên một đường thẳng.
Vậy nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng.
b)
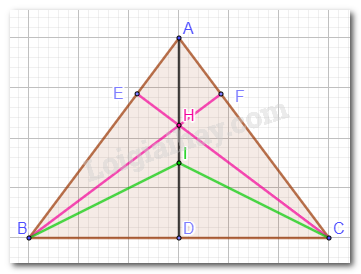
Ta có: \(AD \bot BC\).
H là trực tâm của tam giác ABC nên A, H, D thẳng hàng.
Mà A, H, I thẳng hàng nên A, H, I, K thẳng hàng.
Suy ra: AD là tia phân giác của góc BAC (Vì AI là tia phân giác của góc BAC ).
Nên \(\widehat {BAD} = \widehat {CAD}\).
Xét tam giác BAD và tam giác CAD có:
\(\widehat {BAD} = \widehat {CAD}\);
AD chung;
\(\widehat {ADB} = \widehat {ADC}\) (\(AD \bot BC\)).
\(\Rightarrow \Delta ABD = \Delta ACD\)(g.c.g). Suy ra: AB = AC ( 2 cạnh tương ứng) .
Do đó, tam giác ABC cân tại A
Vậy nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A .