Giải Bài 95 trang 97 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC có trực tâm H đồng thời cũng là điểm cách đều ba đỉnh của tam giác. Tính số đo các góc của tam giác ABC.
Đề bài
Cho tam giác ABC có trực tâm H đồng thời cũng là điểm cách đều ba đỉnh của tam giác. Tính số đo các góc của tam giác ABC.
Phương pháp giải - Xem chi tiết
Sử dụng điều kiện đề bài đưa ra chứng minh tam giác ABC là tam giác đều duy ra mỗi góc của tam giác ABC bằng 60o
Lời giải chi tiết
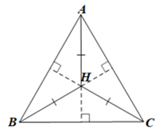
Gọi M là giao điểm của AH và BC.
Vì H cách đều ba đỉnh của tam giác ABC nên HA = HB = HC.
Do HB = HC nên H nằm trên đường trung trực của đoạn thẳng BC.
Tam giác ABC có trực tâm H nên AH ⊥ BC tại M.
Do đó AH là đường trung trực của BC và M là trung điểm của BC.
Khi đó MB = MC.
Xét ∆ABM và ∆ACM có:
^AMB=^AMC(=90∘)
AM là cạnh chung,
MB = MC (chứng minh trên).
Do đó ∆ABM = ∆ACM (hai cạnh góc vuông)
Suy ra AB = AC (hai cạnh tương ứng).
Chứng minh tương tự ta cũng có: AB = BC.
Do đó AB = BC = AC nên tam giác ABC là tam giác đều.
Suy ra ba góc của tam giác ABC đều có số đo bằng 60°.
Vậy số đo các góc của tam giác ABC đều bằng 60°.