Giải Bài 92 trang 97 sách bài tập toán 7 - Cánh diều — Không quảng cáo

Đề bài

Cho tam giác ABC có AB > AC > BC và H là trực tâm. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) H là giao điểm ba đường trung trực của tam giác ABC.

b) CH vuông góc với AB.

c) AH vuông góc với BC.

Lời giải chi tiết

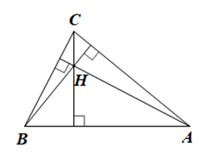
Vì H là trực tâm của tam giác ABC nên H là giao điểm của ba đường cao trong tam giác ABC.

Do đó phát biểu a là sai.

Vì H là trực tâm của tam giác ABC nên CH ⊥ AB. Do đó phát biểu b là đúng.

Vì H là trực tâm của tam giác ABC nên AH ⊥ BC. Do đó phát biểu c là đúng.

Vậy phát biểu a là sai, phát biểu b và c là đúng.