Giải bài tập 1. 27 trang 36 SGK Toán 12 tập 1 - Cùng khám phá — Không quảng cáo

Đề bài

Trong Vật lý, điện trở tương đương ${R_{td}}$ của hai điện trở ${R_1},{R_2}$ mắc song song được xác định bởi công thức$\frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}$. Biết rằng ${R_2} = 3\Omega$. Đặt ${R_1} = x(\Omega ),x > 0$.

a) Tính ${R_{td}}$ theo $x$, xem biểu thức tính được này là một hàm số $y = f(x)$. Khảo sát sự biến thiên và vẽ đồ thị hàm số $f(x)$ với $x > 0$.

b) Khi $x$ tăng, điện trở ${R_{td}}$ thay đổi như thế nào? ${R_{td}}$ không thể vượt qua giá trị bao nhiêu?

Lời giải chi tiết

a)

- Tính ${R_{td}}$ theo $x$ :

$\begin{array}{l}\frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} = \frac{1}{x} + \frac{1}{3}\\\frac{1}{{{R_{td}}}} = \frac{{3 + x}}{{3x}}\\{R_{td}} = \frac{{3x}}{{3 + x}}\end{array}$

Vậy hàm số cần khảo sát là: $y = f(x) = \frac{{3x}}{{3 + x}}$

- Tập xác định: $D = \{ x > 0,x \in R\}$

- Đạo hàm: ${f^\prime }(x) = \frac{d}{{dx}}\left( {\frac{{3x}}{{3 + x}}} \right) = \frac{{3(3 + x) - 3x}}{{{{(3 + x)}^2}}} = \frac{9}{{{{(3 + x)}^2}}} > 0\forall x \in R$

Suy ra hàm số đồng biến trên khoảng $(0, + \infty )$.

- Giới hạn:

$\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{3x}}{{3 + x}} = 0$

$\mathop {\lim }\limits_{x \to  + \infty } f(x) = \mathop {\lim }\limits_{x \to  + \infty } \frac{{3x}}{{3 + x}} = 3$

- Vẽ đồ thị:

Đồ thị hàm số 𝑓(𝑥) là đường cong đi qua các điểm (0,0) và (𝑥,𝑦) với 𝑥>0, tiệm cận ngang 𝑦=3.

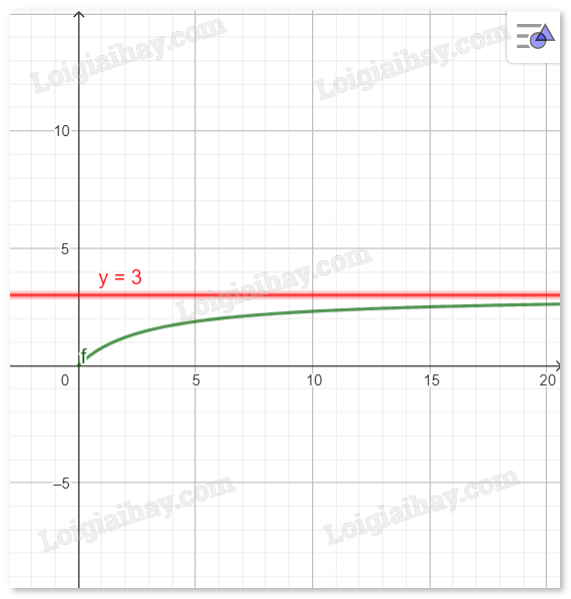
b)

- Khi x tăng, ${R_{td}}$ cũng tăng nhưng tiệm cận về giá trị 3.

- Vậy, ${R_{td}}$ không thể vượt quá giá trị 3.