Giải bài tập 1. 24 trang 35 SGK Toán 12 tập 1 - Cùng khám phá — Không quảng cáo

Đề bài

Một chất điểm chuyển động theo quy luật $s(t) =  - {t^3} + 2t - t$, với 𝑡 (đơn vị: giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và 𝑠 (đơn vị: mét) là quãng đường chất điểm di chuyển được trong khoảng thời gian đó.

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số 𝑠=𝑠(𝑡) trên hệ trục tọa độ 𝑡0𝑠.

b) Trong khoảng thời gian 2 giây kể từ khi bắt đầu chuyển động, chất điểm đạt được vận tốc lớn nhất là bao nhiêu?

Lời giải chi tiết

a)

- Tập xác định: $D = \{ x \ge 0,x \in R\}$

- Tính đạo hàm: $s'(t) =  - 3{t^2} + 4t - 1$

Giải phương trình: $s'(t) = 0 \Leftrightarrow  - 3{t^2} + 4t - 1 = 0 \Rightarrow {t_1} = 1,{t_2} = \frac{1}{3}$

- Giới hạn

$\mathop {\lim }\limits_{t \to \infty } s(t) = \mathop {\lim }\limits_{t \to \infty } \left( { - {t^3} + 2{t^2} - t} \right) =  - \infty$

- Bảng biến thiên:

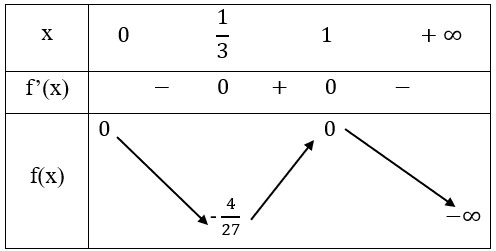
- Vẽ đồ thị

Hàm số nghịch biến trên khoảng (0, $\frac{1}{3}$) và (1,∞)

Hàm số đồng biến trên khoảng ($\frac{1}{3}$,1)

Cực trị: Hàm số đạt cực tiểu tại $x = \frac{1}{2},{y_{CT}} =  - \frac{4}{{27}}$

Hàm số đạt cực đại tại $x = 1,{y_{CD}} = 0$

b)

Ta có vận tốc: $v(t) = s'(t) =  - 3{t^2} + 4t - 1$

Điểm cực trị của vận tốc:

Giải $s''(t) = 0$: $- 6t + 4 = 0 \Rightarrow t = \frac{2}{3}$

Vận tốc tại các điểm biên và cực trị:

$\begin{array}{l}v(0) =  - {3.0^2} + 4.0 - 1 =  - 1\\v\left( {\frac{2}{3}} \right) =  - 3{\left( {\frac{2}{3}} \right)^2} + 4\left( {\frac{2}{3}} \right) - 1 =  - \frac{{12}}{9} + \frac{8}{3} - 1 =  - \frac{4}{3} + \frac{8}{3} - 1 = \frac{1}{3}\\v(2) =  - 3 \cdot {2^2} + 4 \cdot 2 - 1 =  - 12 + 8 - 1 =  - 5\end{array}$

Vậy, vận tốc lớn nhất trong khoảng thời gian 2 giây là $\frac{1}{3}$ m/s.