Giải bài tập 1.26 trang 36 SGK Toán 12 tập 1 - Cùng khám phá
Người ta cần thiết kế một cái lon có dạng hình trụ có thể tích là 1 lít (Hình 1.41). Tính tỉ lệ chiều cao và bán kính đáy hình trụ này để tổng chi phí làm vỏ lon (bao gồm cả hai đáy) là nhỏ nhất.
Đề bài
Người ta cần thiết kế một cái lon có dạng hình trụ có thể tích là 1 lít (Hình 1.41). Tính tỉ lệ chiều cao và bán kính đáy hình trụ này để tổng chi phí làm vỏ lon (bao gồm cả hai đáy) là nhỏ nhất.
Phương pháp giải - Xem chi tiết
- Đặt bán kính đáy là 𝑟 và chiều cao là ℎ của hình trụ.
- Tính diện tích toàn phần của hình trụ dựa trên bán kính và chiều cao.
- Viết hàm chi phí cần tối ưu và điều kiện ràng buộc.
- Khảo sát hàm chi phí để tìm giá trị tối ưu.
Lời giải chi tiết
Gọi bán kính đáy là 𝑟 (𝑟 >0) và chiều cao là ℎ (ℎ>0) của hình trụ.
Thể tích hình trụ: \(V = \pi {r^2}h = 1000(c{m^3})\)
Diện tích xung quanh của hình trụ là: \({A_{xq}} = 2\pi rh\)
Diện tích của hai đáy là: \({A_{2đáy}} = 2\pi {r^2}\)
Tổng diện tích bề mặt: \(A = {A_{xq}} + {A_{2d\'a y}} = 2\pi rh + 2\pi {r^2} = 2\pi r.\frac{{1000}}{{\pi {r^2}}} + 2\pi {r^2} = \frac{{2000}}{r} + 2\pi {r^2}\)
Tìm giá trị cực trị: \(f(r) = \frac{{2000}}{r} + 2\pi {r^2}\)
- Tính đạo hàm: \(f'(r) = - \frac{{2000}}{{{r^2}}} + 4\pi r\)
- Cho đạo hàm bằng 0: \( - \frac{{2000}}{{{r^2}}} + 4\pi r = 0 \Rightarrow 4\pi r = \frac{{2000}}{{{r^2}}} \Rightarrow {r^3} = \frac{{2000}}{{4\pi }} = \frac{{500}}{\pi } \Rightarrow r \simeq 5,42(cm)\)
Bảng biến thiên:
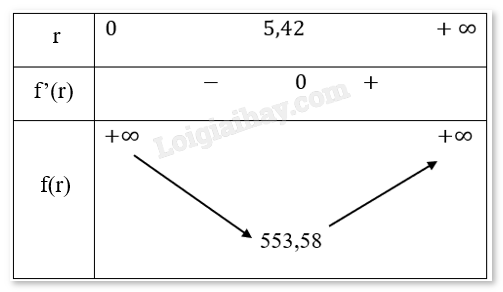
Nhận thấy f(r) đạt giá trị nhỏ nhất tại r ≈ 5,42
Vậy để tổng chi phí làm vỏ lon nhỏ nhất thì:
- Bán kính đáy của hình trụ: r ≈ 5,42 cm
- Chiều cao của hình trụ: \(h = \frac{{1000}}{{\pi {r^2}}} = \frac{{1000}}{{3,14.{{(5,42)}^2}}} \approx 10,84\)cm
- Tỉ lệ chiều cao và bán kính: \(\frac{h}{r} \approx \frac{{10,84}}{{5,42}} \approx 2\)