Giải bài tập 1.20 trang 34 SGK Toán 12 tập 1 - Cùng khám phá
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau: a) (y = {x^3} + 3{x^2} - 4) b) (y = {x^3} + 4{x^2} + 4x) c) (y = - 2{x^3} + 2) d) (y = - {x^3} - {x^2} - x + 1)
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau:
a) \(y = {x^3} + 3{x^2} - 4\)
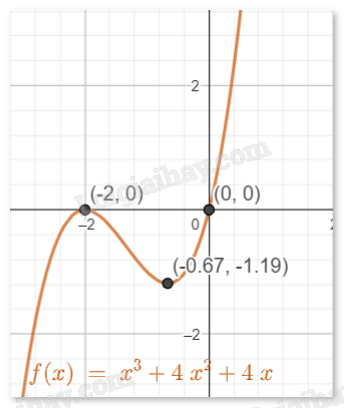
b) \(y = {x^3} + 4{x^2} + 4x\)
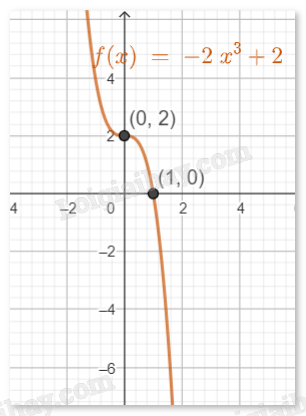
c) \(y = - 2{x^3} + 2\)
d) \(y = - {x^3} - {x^2} - x + 1\)
Phương pháp giải - Xem chi tiết
- Tìm tập xác định của hàm số
- Xét sự biến thiên của hàm số
- Vẽ đồ thị hàm số
Lời giải chi tiết
a)
- Tập xác định: D = R.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^3} + 3{x^2} - 4} \right) = \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} + 3{x^2} - 4} \right) = - \infty \)
Ta có: \({y^\prime } = 3{x^2} + 6x\)
\({y^\prime } = 0 \leftrightarrow 3{x^2} + 6x = 0 \leftrightarrow x = - 2{\rm{ hoac }}x = 0\)
Bảng biến thiên:
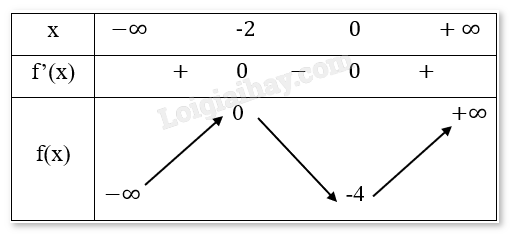
Chiều biến thiên: Hàm số đồng biến trên các khoảng (−∞,-2) và (0,∞), nghịch biến trên khoảng (-2,0).
Cực trị: Hàm số đạt cực tiểu tại \(x = 0,{y_{CT}} = - 4\)
Hàm số đạt cực đại tại \(x = - 2,{y_{CD}} = 0\)
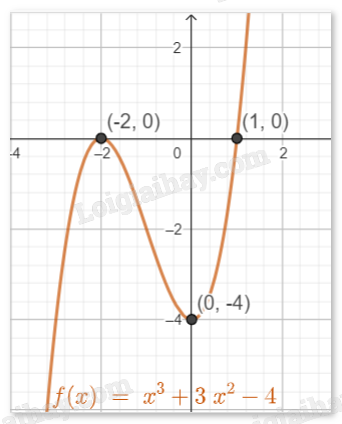
- Vẽ đồ thị:
Giao điểm với trục Oy là (0,-4).
Giao điểm với trục Ox là (-2,0), (1,0).
b)
- Tập xác định: D = R.
- Sự biến thiên:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^3} + 4{x^2} + 4x} \right) = \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} + 4{x^2} + 4x} \right) = - \infty \)
Ta có: \({y^\prime } = 3{x^2} + 8x + 4\)
\({y^\prime } = 0 \leftrightarrow 3{x^2} + 8x + 4 = 0 \leftrightarrow x = - 2{\rm{ }}\)hoặc \(x = \frac{{ - 2}}{3}\)
Bảng biến thiên:
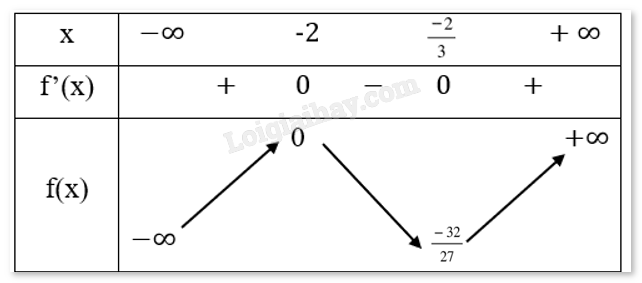
Chiều biến thiên: Hàm số đồng biến trên các khoảng \(( - \infty , - 2)\) và \(\left( {\frac{{ - 2}}{3},\infty } \right)\), nghịch biến trên khoảng \(\left( { - 2,\frac{{ - 2}}{3}} \right)\).
Cực trị: Hàm số đạt cực tiểu tại \(x = \frac{{ - 2}}{3},{y_{CT}} = - \frac{{32}}{{27}}\)
Hàm số đạt cực đại tại \(x = - 2,{y_{CD}} = 0\)
- Vẽ đồ thị:
Đi qua gốc tọa độ O(0,0).
Giao điểm với trục Ox là (-2,0).
c)
- Tập xác định: D = R.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - 2{x^3} + 2} \right) = - \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } y{\rm{ }} = \mathop {\lim }\limits_{x \to - \infty } \left( { - 2{x^3} + 2} \right) = \infty \)
Ta có: \({y^\prime } = - 6{x^2} \le 0\forall x \in R\)
\({y^\prime } = 0 \leftrightarrow - 6x = 0 \leftrightarrow x = 0{\rm{ }}\)
Bảng biến thiên:
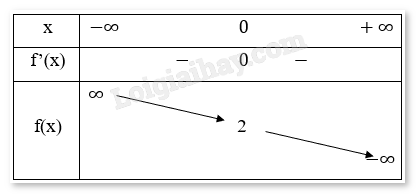
Chiều biến thiên: Hàm số nghịch biến trên R.
Cực trị: Hàm số không có cực trị
- Vẽ đồ thị:
Giao điểm với trục Oy là (0,2).
Giao điểm với trục Ox là (1,0).
d) \(\)
- Tập xác định: D = R.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - {x^3} - {x^2} - x + 1} \right) = - \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } y{\rm{ }} = \mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} - {x^2} - x + 1} \right) = \infty \)
Ta có: \({y^\prime } = - 3{x^2} - 2x - 1 < 0\forall x \in R\)
Bảng biến thiên:
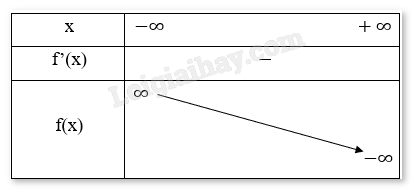
Chiều biến thiên: Hàm số nghịch biến trên R.
Cực trị: Hàm số không có cực trị
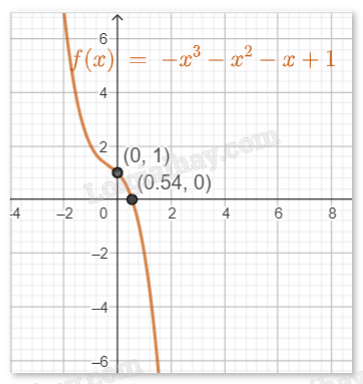
- Vẽ đồ thị
Giao với trục Oy tại điểm (0,1)
Giao với trục Ox tại điểm (0.5437,0)