Giải bài tập 1.17 trang 22 SGK Toán 12 tập 1 - Cùng khám phá
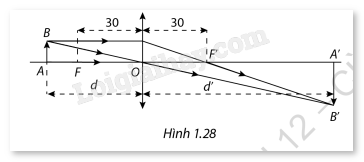
Một thấu kính hội tụ có tiêu cự f=30cm như hình 1.28. Trong vật lý, ta biết rằng nếu đặt vật thật AB cách quang tâm O của thấu kính một khoảng d(cm) lơn hơn 30cm thì được ảnh thật A’B’ cách quang tâm của thấu kính một khoảng d’(cm). Ngược lại, nếu 0<d<30 thì ta có ảnh ảo. Công thức thấu kính là \(\frac{1}{d} + \frac{1}{{d'}} = \frac{{\rm{1}}}{{\rm{f}}}\). a) Từ công thức thấu kính, tìm biểu thức xác định d’ theo d. b) Xem biểu thức của d’ ở câu a là một hàm số theo d, kí hiệu là h(d). Tìm các
Đề bài
Một thấu kính hội tụ có tiêu cự f=30cm như hình 1.28. Trong vật lý, ta biết rằng nếu đặt vật thật AB cách quang tâm O của thấu kính một khoảng d(cm) lơn hơn 30cm thì được ảnh thật A’B’ cách quang tâm của thấu kính một khoảng d’(cm). Ngược lại, nếu 0<d<30 thì ta có ảnh ảo. Công thức thấu kính là \(\frac{1}{d} + \frac{1}{{d'}} = \frac{{\rm{1}}}{{\rm{f}}}\) .
a) Từ công thức thấu kính, tìm biểu thức xác định d’ theo d.
b) Xem biểu thức của d’ ở câu a là một hàm số theo d, kí hiệu là h(d). Tìm các đường tiệm cận của h(d).
Phương pháp giải - Xem chi tiết
Từ công thức \(\frac{1}{d} + \frac{1}{{d'}} = \frac{{\rm{1}}}{{\rm{f}}}\) rút ra d’.
Tìm \(h\left( d \right)\;\), \(h\left( d \right)\;\).
Lời giải chi tiết
a) Ta có: \(\frac{1}{d} + \frac{1}{{d'}} = \frac{{\rm{1}}}{{\rm{f}}} = \frac{1}{{30}}\)
\( \Rightarrow \frac{1}{{d'}} = \frac{{\rm{1}}}{{30}} - \frac{1}{d} = \frac{{d - 30}}{{30d}}\)
\( \Rightarrow d' = \frac{{30d}}{{d - 30}}\)
b) Ta có \(h(d) = \frac{{30d}}{{d - 30}}\)
c) \(\mathop {\lim }\limits_{d \to + \infty } h\left( d \right)\;\; = \mathop {\lim }\limits_{d \to + \infty } \frac{{30}}{{1 - \frac{3}{d}}} = 30\;\)
Suy ra y = 30 là đường tiệm cận ngang của hàm số.
\(\mathop {\lim }\limits_{d \to {{30}^ + }} h\left( d \right)\;\; = \mathop {\lim }\limits_{d \to {{30}^ + }} \frac{{30d}}{{d - 30}} = + \infty \;,\mathop {\lim }\limits_{d \to {{30}^ - }} h\left( d \right)\;\; = \mathop {\lim }\limits_{d \to {{30}^ - }} \frac{{30d}}{{d - 30}} = - \infty \;\)
Suy ra x = 30 là đường tiệm cận đứng của h(d).