Giải bài tập 1.14 trang 21 SGK Toán 12 tập 1 - Cùng khám phá
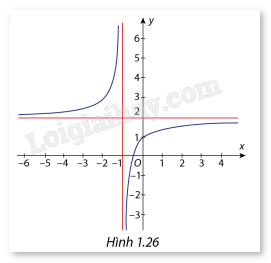
Cho hàm số (y = frac{{2x + 1}}{{x + 1}}) có đồ thị là đường cong như hình 1.26. Xác định phương trình đường tiệm cận đứng, đường tiệm cận ngang của hàm số.
Đề bài
Cho hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) có đồ thị là đường cong như hình 1.26. Xác định phương trình đường tiệm cận đứng, đường tiệm cận ngang của hàm số.
Phương pháp giải - Xem chi tiết
Xét \(\mathop {\lim }\limits_{x \to + \infty } y,\mathop {\lim }\limits_{x \to - \infty } y,\mathop {\lim }\limits_{x \to {2^ - }} y,\mathop {\lim }\limits_{x \to {2^ + }} y\).
Lời giải chi tiết
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 1}}{{x + 1}} = 2,\mathop {\lim }\limits_{x \to - \infty } \frac{{2x + 1}}{{x + 1}} = 2\).
Suy ra đường thẳng \(y = 2\) là đường tiệm cận ngang của hàm số.
Ta có: \(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{2x + 1}}{{x + 1}} = - \infty ,\mathop {\lim }\limits_{x \to - {1^ - }} \frac{{2x + 1}}{{x + 1}} = + \infty \).\(\)
Suy ra đường thẳng \(x = - 1\) là đường tiệm cận đứng của hàm số.