Giải bài tập 1.6 trang 14 SGK Toán 12 tập 1 - Kết nối tri thức
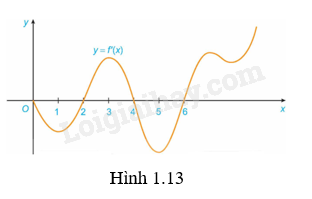
Đồ thị của đạo hàm bậc nhất (y = f'left( x right)) của hàm số f(x) được cho trong Hình 1.13: a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích. b) Tại giá trị nào của x thì f(x) có cực đại hoặc cực tiểu? Giải thích.
Đề bài
Đồ thị của đạo hàm bậc nhất \(y = f'\left( x \right)\) của hàm số f(x) được cho trong Hình 1.13: a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích. b) Tại giá trị nào của x thì f(x) có cực đại hoặc cực tiểu? Giải thích.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Sử dụng kiến thức về định lí cực trị hàm số để giải: Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực tiểu của hàm số f(x).
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực đại của hàm số f(x).
Lời giải chi tiết
a) Vì \(f'\left( x \right) > 0\) khi \(x \in \left( {2;4} \right)\) và \(x \in \left( {6; + \infty } \right)\). Do đó, hàm số f(x) đồng biến trên \(\left( {2;4} \right)\) và \(\left( {6; + \infty } \right)\).
Vì \(f'\left( x \right) < 0\) khi \(x \in \left( {0;2} \right)\) và \(x \in \left( {4;6} \right)\). Do đó, hàm số f(x) nghịch biến trên \(\left( {0;2} \right)\) và \(\left( {4;6} \right)\).
b) Vì \(f'\left( x \right) < 0\) với mọi \(x \in \left( {0;2} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {2;4} \right)\) nên \(x = 2\) là một điểm cực tiểu của hàm số f(x).
Vì \(f'\left( x \right) > 0\) với mọi \(x \in \left( {2;4} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {4;6} \right)\) nên điểm \(x = 4\) là một điểm cực đại của hàm số f(x).
Vì \(f'\left( x \right) < 0\) với mọi \(x \in \left( {4;6} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {6; + \infty } \right)\) nên điểm \(x = 6\) là một điểm cực tiểu của hàm số f(x).