Giải bài tập 2 trang 88 SGK Toán 12 tập 1 - Cánh diều — Không quảng cáo

Đề bài

Bảng 9 biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của 1 công ty (đơn vị: triệu đồng)

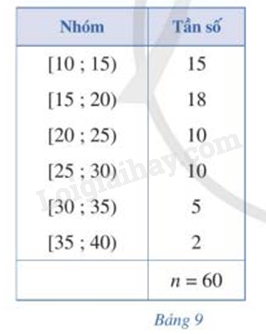
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó

b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó

Lời giải chi tiết

a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: $R = 40 - 10 = 30$

b) Số phần tử của mẫu là n = 60

Tần số tích lũy của các nhóm lần lượt là $c{f_1} = 15$, $c{f_2} = 33$, $c{f_3} = 43$, $c{f_4} = 53$, $c{f_5} = 58$, $c{f_6} = 60$

Ta có: $\frac{n}{4} = \frac{{60}}{4} = 15$ suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bẳng 15. Xét nhóm 1 là nhóm [10;15] có s = 10, h = 5, ${n_1} = 15$

Ta có tứ phân vị thứ nhất là: ${Q_1} = s + \left( {\frac{{15 - c{f_0}}}{{{n_1}}}} \right).h = 10 + \left( {\frac{{15 - 0}}{{15}}} \right).5 = 15$

Ta có: $\frac{{3n}}{4} = \frac{{3.60}}{4} = 45$ mà 43 < 45 < 53 suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bẳng 45. Xét nhóm 4 là nhóm [25;30] có t = 25, l = 5, ${n_4} = 10$và nhóm 3 là nhóm [20;25] có $c{f_3} = 43$

Ta có tứ phân vị thứ ba là: ${Q_3} = t + \left( {\frac{{45 - c{f_3}}}{{{n_4}}}} \right).l = 25 + \left( {\frac{{45 - 43}}{{10}}} \right).5 = 26$

Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là: ${Q_3} - {Q_1} = 26 - 15 = 9$