Giải bài tập 2 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung $\overset\frown{BD};\overset\frown{BE};\overset\frown{EC}$.

Lời giải chi tiết

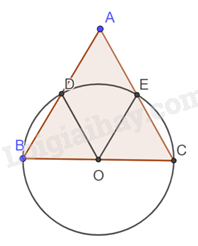
Gọi O là tâm đường tròn đường kính BC.

Ta có OB = OD (= R)

Vậy tam giác BOD cân tại O

Mà $\widehat {DBO}$= 60 ^o nên tam giác BOD đều

Suy ra $\widehat {DOB}$= 60 ^o

OE = DC (= R)

Vậy tam giác EOC cân tại O

Mà $\widehat {ECO}$= 60 ^o nên tam giác EOC đều

Suy ra $\widehat {EOC}$= 60 ^o

Ta có $\widehat {BOD} + \widehat {DOE} + \widehat {EOC} = {180^o}$

Suy ra 60 ^o + $\widehat {DOE} + {60^o} = {180^o}$ nên $\widehat {DOE} = {60^o}$

Vì $\widehat {BOD} = \widehat {DOE} = \widehat {EOC} = {60^o}$ nên sđ$\overset\frown{BD}$ = sđ$\overset\frown{BE}$ = sđ$\overset\frown{EC}={{60}^{o}}$

Vậy $\overset\frown{BD}=\overset\frown{BE}=\overset\frown{EC}$