Giải bài tập 5.10 trang 106 SGK Toán 9 tập 1 - Cùng khám phá
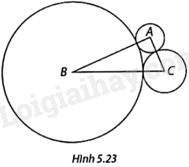
Ba đường tròn (A; 2), (B; 10) và (C; 3) đôi một tiếp xúc ngoài nhau như trong Hình 5.23. Chứng minh rằng \(\Delta ABC\) là tam giác vuông.
Đề bài
Ba đường tròn (A; 2), (B; 10) và (C; 3) đôi một tiếp xúc ngoài nhau như trong Hình 5.23. Chứng minh rằng \(\Delta ABC\) là tam giác vuông.
Phương pháp giải - Xem chi tiết
Cho hai đường tròn phân biệt (O; R) và (O’; r) và \(d = OO'\). Nếu \(d = R + r\) thì hai đường tròn tiếp xúc ngoài.
Lời giải chi tiết
Vì ba đường tròn (A; 2), (B; 10) và (C; 3) đôi một tiếp xúc ngoài nhau nên
\(\begin{array}{l}AC = 2 + 3 = 5,\\BC = 10 + 3 = 13,\\AB = 10 + 2 = 12.\end{array}\)
Vì \(A{B^2} + A{C^2} = B{C^2}\) (vì \({5^2} + {12^2} = {13^2}\)) nên \(\Delta ABC\) là tam giác vuông tại A (định lí Pythagore đảo)
Cùng chủ đề:
Giải bài tập 5. 10 trang 106 SGK Toán 9 tập 1 - Cùng khám phá