Giải bài tập 5.14 trang 110 SGK Toán 9 tập 1 - Cùng khám phá
Cho đường tròn tâm O bán kính R và một điểm A nằm trong (O) \(\left( {OA < R} \right)\). Vẽ đường thẳng a bất kì đi qua A. Xác định vị trí tương đối của đường thẳng a và đường tròn (O).
Đề bài
Cho đường tròn tâm O bán kính R và một điểm A nằm trong (O) \(\left( {OA < R} \right)\). Vẽ đường thẳng a bất kì đi qua A. Xác định vị trí tương đối của đường thẳng a và đường tròn (O).
Phương pháp giải - Xem chi tiết
Cho đường tròn (O; R) và đường thẳng a. Đặt d là khoảng cách từ O đến đường thẳng a. Vị trí tương đối của đường thẳng a và đường tròn (O; R) có thể được xác định dựa vào mối quan hệ giữa R và d như sau:
+ Nếu \(d > R\) thì đường thẳng a và đường tròn (O) không giao nhau.
+ Nếu \(d = R\) thì đường thẳng a và đường tròn (O) tiếp xúc nhau.
+ Nếu \(d < R\) thì đường thẳng a và đường tròn (O) cắt nhau.
Lời giải chi tiết
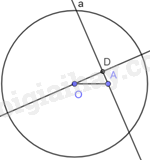
Qua O dựng đường thẳng vuông góc với đường thẳng a tại D. Khi đó, OD là khoảng cách từ điểm O đến đường thẳng a.
Vì \(OD \bot a\) tại D nên tam giác OAD vuông tại D. Do đó, \(OD < OA\).
Mà \(OA < R\) nên \(OD < R\).
Do đó, đường thẳng a và đường tròn (O) cắt nhau.