Giải bài tập 5.17 trang 114 SGK Toán 9 tập 1 - Cùng khám phá
Cho A là một điểm thuộc đường tròn (O), M là một điểm thuộc tiếp tuyến của (O) tại điểm A (M khác A). Đường tròn tâm M bán kính MA cắt (O) tại B (B khác A). Chứng minh rằng MB là một tiếp tuyến của (O).
Đề bài
Cho A là một điểm thuộc đường tròn (O), M là một điểm thuộc tiếp tuyến của (O) tại điểm A (M khác A). Đường tròn tâm M bán kính MA cắt (O) tại B (B khác A). Chứng minh rằng MB là một tiếp tuyến của (O).
Phương pháp giải - Xem chi tiết
+ Chứng minh \(\widehat {MAO} = {90^o}\).
+ Chứng minh \(\Delta AMO = \Delta BMO\left( {c.c.c} \right)\) nên \(\widehat {MAO} = \widehat {MBO} = {90^o}\).
+ Suy ra \(MB \bot BO\) tại B. Mà B thuộc đường tròn (O) nên MB là tiếp tuyến của (O).
Lời giải chi tiết
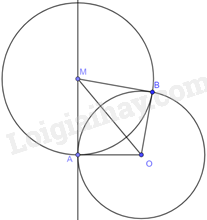
Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\) nên \(\widehat {MAO} = {90^o}\).
Tam giác AMO và tam giác BMO có:
\(OA = OB\) (bán kính (O)), \(MA = MB\) (bán kính (M)), OM chung.
Do đó, \(\Delta AMO = \Delta BMO\left( {c.c.c} \right)\) nên \(\widehat {MAO} = \widehat {MBO} = {90^o}\)
Suy ra \(MB \bot BO\) tại B. Mà B thuộc đường tròn (O) nên MB là tiếp tuyến của (O).