Giải bài tập 5.21 trang 114 SGK Toán 9 tập 1 - Cùng khám phá
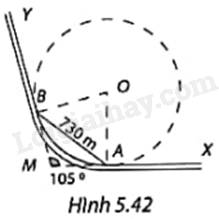
Trong Hình 5.42, để tàu không trật bánh ray khi chuyển hướng từ đường ray thẳng XA sang đường ray thẳng YB, đoạn ray nối được thiết kế là một phần của đường tròn (O) tiếp xúc với XA tại A và BY tại B. Biết góc chuyển hướng của tàu là ^AMB=105o và khoảng cách giữa hai điểm A và B là 730m. Tính bán kính của đường tròn (O). Làm tròn kết quả đến đơn vị mét.
Đề bài
Trong Hình 5.42, để tàu không trật bánh ray khi chuyển hướng từ đường ray thẳng XA sang đường ray thẳng YB, đoạn ray nối được thiết kế là một phần của đường tròn (O) tiếp xúc với XA tại A và BY tại B. Biết góc chuyển hướng của tàu là ^AMB=105o và khoảng cách giữa hai điểm A và B là 730m. Tính bán kính của đường tròn (O). Làm tròn kết quả đến đơn vị mét.
Phương pháp giải - Xem chi tiết
+ Sử dụng tính chất hai tiếp tuyến cắt nhau suy ra MA=MB, ^AMO=^BMO=12^BMA.
+ Chứng minh MO là đường trung trực của AB.
+ Gọi I là trung điểm của AB thì AI=AB2 và MO vuông góc với AB tại I.
+ Chứng minh tam giác MAO vuông tại A, tính góc MOA.
+ Tam giác AIO vuông tại I nên AI=AO.sinIOA, từ đó tính được AO.
Lời giải chi tiết
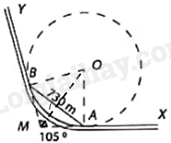
Vì MA, MB là tiếp tuyến của (O) nên:
+ MA=MB.
+ MO là tia phân giác góc BMA nên
^AMO=^BMO=12^BMA=52,5o.
Vì OA=OB (bán kính (O)) nên O thuộc đường trung trực của AB.
Vì MA=MB nên M thuộc đường trung trực của AB.
Do đó, MO là đường trung trực của AB.
Gọi I là trung điểm của AB thì AI=7302=365(m) và MO vuông góc với AB tại I.
Vì MA là tiếp tuyến của (O) nên MA⊥AO
Suy ra, tam giác MOA vuông tại A nên ^MOA=90o−^AMO=37,5o
Tam giác AIO vuông tại I nên AI=AO.sinIOA,
suy ra AO=AIsinIOA=365sin37,5o≈600(m).
Vậy bán kính đường tròn (O) khoảng 600m.