Giải bài tập 5.24 trang 121 SGK Toán 9 tập 1 - Cùng khám phá
Tiếp tuyến tại hai điểm A và B của đường tròn (O) cắt nhau tại M. Biết rằng MAB là tam giác đều. Tính số đo cung nhỏ và cung lớn AB.
Đề bài
Tiếp tuyến tại hai điểm A và B của đường tròn (O) cắt nhau tại M. Biết rằng MAB là tam giác đều. Tính số đo cung nhỏ và cung lớn AB.
Phương pháp giải - Xem chi tiết
+ Chứng minh \(\widehat {MAO} = \widehat {MBO} = {90^o}\), \(\widehat {AMB} = {60^o}\).
+ Tứ giác MAOB có: \(\widehat {MAO} + \widehat {MBO} + \widehat {AMB} + \widehat {AOB} = {360^o}\), từ đó tính góc AOB.
+ Số đo cung nhỏ AB bằng số đo góc AOB, số đo cung AB lớn bằng hiệu giữa 360 độ và số đo cung nhỏ AB.
Lời giải chi tiết
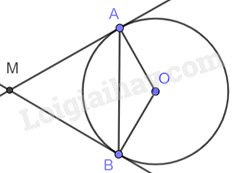
Vì MA và MB là tiếp tuyến của (O) nên \(MA \bot AO,MB \bot BO\), suy ra \(\widehat {MAO} = \widehat {MBO} = {90^o}\).
Vì tam giác MAB đều nên \(\widehat {AMB} = {60^o}\)
Tứ giác MAOB có:
\(\widehat {MAO} + \widehat {MBO} + \widehat {AMB} + \widehat {AOB} = {360^o}\)
\(\widehat {AOB} = {360^o} - \left( {\widehat {MAO} + \widehat {MBO} + \widehat {AMB}} \right) = {360^o} - \left( {{{90}^o} + {{90}^o} + {{60}^o}} \right) = {120^o}\)
Vì AOB là góc ở tâm chắn cung nhỏ AB nên số đo cung nhỏ AB bằng \({120^o}\).
Số đo cung AB lớn là:
\({360^o} - {120^o} = {240^o}\).