Giải bài tập 5.26 trang 121 SGK Toán 9 tập 1 - Cùng khám phá
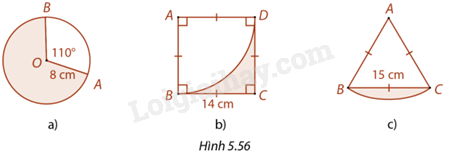
Tính chu vi và diện tích phần được tô màu trong mỗi trường hợp ở Hình 5.56. Làm tròn kết quả đến hàng phần mười.
Đề bài
Tính chu vi và diện tích phần được tô màu trong mỗi trường hợp ở Hình 5.56. Làm tròn kết quả đến hàng phần mười.
Phương pháp giải - Xem chi tiết
Công thức tính độ dài cung \({n^o}\) của đường tròn bán kính R: \(l = \frac{{\pi Rn}}{{180}}\).
Công thức tính diện tích hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{{\pi {R^2}n}}{{360}}\).
Lời giải chi tiết
a) Góc AOB là góc ở tâm chắn cung nhỏ AB nên số đo cung AB nhỏ là bằng 110 độ.
Khi đó, số đo cung AB lớn bằng:
\({360^o} - {110^o} = {250^o}\).
Phần được tô màu là hình quạt tâm O, cung lớn AB nên
+ Diện tích phần tô màu là:
\(S = \frac{{\pi {{.8}^2}.250}}{{360}} = \frac{{400\pi }}{9} \approx 139,6\left( {c{m^2}} \right)\)
+ Độ dài cung AB lớn là:
\({l_{AB}} = \frac{{\pi .8.250}}{{180}} = \frac{{100\pi }}{9}\left( {cm} \right)\)
+ Chu vi hình được tô màu là:
\(C = OA + OB + {l_{AB}} = 8 + 8 + \frac{{100\pi }}{9} = 16 + \frac{{100\pi }}{9} \approx 50,9\left( {cm} \right)\)
b) Diện tích hình vuông ABCD là:
\({S_{ABCD}} = {14^2} = 196\left( {c{m^2}} \right)\)
Phần không tô màu là \(\frac{1}{4}\) hình tròn bán kính 14cm nên diện tích phần không tô màu là: \({S_1} = \frac{1}{4}{.5^2}.\pi = \frac{{25}}{4}\pi \left( {c{m^2}} \right)\).
Diện tích phần tô màu là:
\(S = {S_{ABCD}} - {S_1} = 196 - \frac{{25\pi }}{4} \approx 176,4\left( {c{m^2}} \right)\)
Độ dài cung BD là:
\({l_{BD}} = \frac{{\pi .14.90}}{{180}} = 7\pi \left( {cm} \right)\)
Chu vi phần được tô màu là:
\(C = DC + CB + {l_{BD}} = 14 + 14 + 7\pi = 28 + 7\pi \approx 50\left( {cm} \right)\)
c) Tam giác ABC có: \(AB = BC = CA\) nên tam giác ABC đều. Do đó, \(\widehat {BAC} = {60^o}\) nên hình quạt tâm A, hai bán kính AB, AC có số đo cung BC bằng 60 độ.
Diện tích hình quạt tâm A, cung BC là:
\({S_q} = \frac{{\pi {{.15}^2}.60}}{{360}} = \frac{{75\pi }}{2}\left( {c{m^2}} \right)\)
Diện tích tam giác đều ABC cạnh 15cm là:
\({S_{ABC}} = \frac{{{{15}^2}\sqrt 3 }}{4} = \frac{{225\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Do đó, diện tích phần được tô màu là:
\(S = {S_q} - {S_{ABC}} = \frac{{75\pi }}{2} - \frac{{225\sqrt 3 }}{4} \approx 20,4\left( {c{m^2}} \right)\)
Độ dài cung BC là:
\({l_{BC}} = \frac{{\pi .15.60}}{{180}} = 5\pi \left( {cm} \right)\).
Chu vi phần được tô màu là:
\({l_{BC}} + BC = 5\pi + 15 \approx 30,7\left( {cm} \right)\).