Giải bài tập 5.15 trang 110 SGK Toán 9 tập 1 - Cùng khám phá
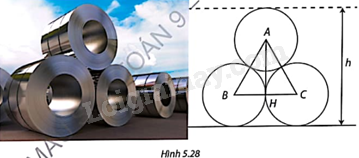
Trong Hình 5.28, các cuộn thép được đặt chồng lên nhau. Đường kính của mỗi cuộn thép là 1,2m. Gọi A, B, C lần lượt là tâm của mặt cắt các cuộn thép, H là tiếp điểm của hai cuộn thép phía dưới. a) Chứng minh \(\Delta ABC\) là tam giác đều và tính độ dài AH. b) Tính khoảng cách từ B và C đến mặt đất. c) Tính chiều cao h của khối ba cuộn thép.
Đề bài
Trong Hình 5.28, các cuộn thép được đặt chồng lên nhau. Đường kính của mỗi cuộn thép là 1,2m. Gọi A, B, C lần lượt là tâm của mặt cắt các cuộn thép, H là tiếp điểm của hai cuộn thép phía dưới.
a) Chứng minh \(\Delta ABC\) là tam giác đều và tính độ dài AH.
b) Tính khoảng cách từ B và C đến mặt đất.
c) Tính chiều cao h của khối ba cuộn thép.
Phương pháp giải - Xem chi tiết
a) + Gọi I là tiếp điểm của mặt cắt của các cuộn thép tâm A và tâm C, K là tiếp điểm của mặt cắt của các cuộn thép tâm A và tâm B.
+ Tính bán kính của các đường tròn (A), (B), (C).
+ Từ đó tính được \(AB = BC = AC\) nên tam giác ABC đều.
+ Chứng minh AH là đường trung tuyến đồng thời là đường cao trong tam giác ABC đều.
+ Áp dụng định lí Pythagore để tính AH.
b) Đường tròn tâm (B), (C) tiếp xúc với mặt đất nên khoảng cách từ B, C đến mặt đất bằng bán kính của đường tròn tâm (B), (C).
c) + Chiều cao của ba cuộn thép bằng tổng đường kính của hai đường tròn tâm A và tâm C.
Lời giải chi tiết
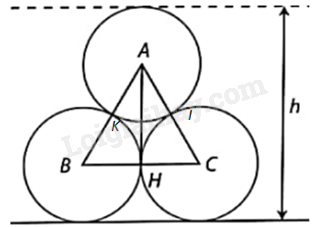
Gọi I là tiếp điểm của mặt cắt của các cuộn thép tâm A và tâm C, K là tiếp điểm của mặt cắt của các cuộn thép tâm A và tâm B.
a) Vì AI, AK là bán kính đường tròn (A) nên
\(AI = AK = \frac{{1,2}}{2} = 0,6m\).
Vì BH, BK là bán kính đường tròn (B) nên
\(BH = BK = \frac{{1,2}}{2} = 0,6m\).
Vì CI, CH là bán kính đường tròn (C) nên
\(CI = CH = \frac{{1,2}}{2} = 0,6m\).
Vì các cuộn thép tâm A, B, C đặt chồng lên nhau nên các mặt cắt của các cuộn thép tâm A, B, C tiếp xúc ngoài nhau.
Do đó, \(AC = AI + IC = 1,2m,BC = BH + HC = 1,2m,AB = BK + AK = 1,2m\)
Suy ra: \(AB = BC = AC\).
Vậy \(\Delta ABC\) là tam giác đều
Mà AH là đường trung tuyến của tam giác ABC (vì \(BH = HC\)) nên AH là đường cao của tam giác ABC. Suy ra, tam giác AHC vuông tại H.
Do đó, \(A{H^2} + H{C^2} = A{C^2}\) (định lí Pythagore), suy ra
\(AH = \sqrt {A{C^2} - A{H^2}} = \sqrt {1,{2^2} - 0,{6^2}} = \frac{{3\sqrt 3 }}{5}\left( m \right)\)
b) Vì đường tròn tâm (B), (C) tiếp xúc với mặt đất nên khoảng cách từ B, C đến mặt đất bằng bán kính của đường tròn tâm (B), (C).
Do đó, khoảng cách từ B và C đến mặt đất đều bằng 0,6m.
c) Vì các cuộn thép tâm A, B, C tiếp xúc ngoài nhau nên chiều cao h của khối ba cuộn thép là: \(h = 1,2 + 1,2 = 2,4\left( m \right)\)